1 solutions
-
1
很好的题目,单调栈+st表+二分/倍增。
题意
非常形象的题目,一个圆盘的水超过容量了就会飞到下面第一个比它大的圆盘。然后往r圆盘注v的水,求水会流到哪里。
每个询问互不干扰!
思路1
首先最简单的模拟,把水会流到哪里用一个数组(To数组)记下来,然后让水一直流,直到水没了。
代码1
#include<iostream> #include<stack> #define nmax 200000 #define qmax 300000 #define lognmax 20 #define inf 0x7fffffff using namespace std; int d[nmax],c[nmax],r[qmax],v[qmax],t[nmax]; int main(){ #ifdef local system(""); int logn=3; #endif //---输入O(n)---// #ifdef local cout<<"\033[32mn,q:\n\033[0m"; #endif int n,q; cin>>n>>q; #ifdef local cout<<"\033[32md,c:\n\033[0m"; #endif for(int i=1;i<=n;i++) cin>>d[i]>>c[i]; #ifdef local cout<<"\033[32mr,v:\n\033[0m"; #endif for(int i=1;i<=q;i++) cin>>r[i]>>v[i]; #ifdef local cout<<"\n"; #endif //---计算To数组O(n^2)---// for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) if(d[j]>d[i]){ t[i]=j; break; } #ifdef local cout<<"\033[32mTo数组:\n\033[0m"; for(int i=1;i<=n;i++) cout<<t[i]<<" "; cout<<"\n"; #endif //---解决并回答O(n^2)---// #ifdef local cout<<"\033[32mans:\n\033[0m"; #endif for(int i=1;i<=q;i++){ while(r[i]&&v[i]>c[r[i]]){ v[i]-=c[r[i]]; r[i]=t[r[i]]; } cout<<r[i]<<"\n"; } //---完结撒花---// return 0; }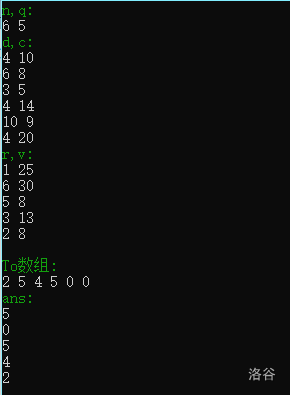
思路2
两个O(n^2)看起来就很头疼,所以我们拆分着看。
首先,先易后难,对于计算To数组,我们把问题剥离出来:
求一个元素前最后一个比它大的。(比它小的就把To标给它)
换句话说,保持一个序列的单调性,不满足单调性的全部滚蛋(然后标To)。
单调栈的出现就是为了解决这个问题!
代码2
#include<iostream> #include<stack> #define nmax 200000 #define qmax 300000 #define lognmax 20 #define inf 0x7fffffff using namespace std; int d[nmax],c[nmax],r[qmax],v[qmax],t[nmax]; int main(){ #ifdef local system(""); int logn=3; #endif //---输入O(n)---// #ifdef local cout<<"\033[32mn,q:\n\033[0m"; #endif int n,q; cin>>n>>q; #ifdef local cout<<"\033[32md,c:\n\033[0m"; #endif for(int i=1;i<=n;i++) cin>>d[i]>>c[i]; #ifdef local cout<<"\033[32mr,v:\n\033[0m"; #endif for(int i=1;i<=q;i++) cin>>r[i]>>v[i]; #ifdef local cout<<"\n"; #endif //---计算To数组O(n)---// stack<int>s; for(int i=1;i<=n;i++){ while(!s.empty()&&d[s.top()]<d[i]){ t[s.top()]=i; s.pop(); } s.push(i); } #ifdef local cout<<"\033[32mTo数组:\n\033[0m"; for(int i=1;i<=n;i++) cout<<t[i]<<" "; cout<<"\n"; #endif //---解决并回答O(n^2)---// #ifdef local cout<<"\033[32mans:\n\033[0m"; #endif for(int i=1;i<=q;i++){ while(r[i]&&v[i]>c[r[i]]){ v[i]-=c[r[i]]; r[i]=t[r[i]]; } cout<<r[i]<<"\n"; } //---完结撒花---// return 0; }理论上栈中剩余元素应该标到水池的(比如样例中的5、6),但是因为全局数组初始化为0所以不用特殊处理,但是如果是开的动态数组或局部数组(其实不会MLE)还没有初始化的同学要记得在结尾加上这一段:
while(!s.empty()){ t[s.top()]=0; s.pop(); }思路3
虽然说To数组的计算被我们降到了,but解决问题还是的时间复杂度。对此,还是同样的方法,剥离问题:
找到一个单调递增序列里的一个值。
为什么这么说呢?首先,看样例1->2->5->0,假设从1出发,1->2的路程一定小于1->5或者1->0的路程,而我们要找的就是值为v的那个点。
把这句话摆出来,pwm都知道要用倍增/二分。
但是问题不是1->2->3->4...的规则链,而且每次起点都不一样(所以路程长度也不一样),那么怎么存放路程呢?
- 每个询问互不干扰!
- 每次起点都不一样。
看算法标签。
是它,就是它!死数据结构,ST表!
我们需要两个st表(因为有两个问题):第一个问题是这个链是不规则的,所以To数组还是很重要的一part,而且要变成st表以供快速查询;第二个问题就是存花费,所以还需要一个st表,表示从i走步所需的水量。
但是这两个st表的推演公式还是要好好看看的。
首先To数组,走步也就等于走步再走步。
(初始化就是原先的To[i]变成To[i][0])
to[i][k]=t[to[i][k-1]][k-1];其次Cost数组有两个初始化。
- cost[i][0]就是c[i]。——你也可以直接
cin>>cost[i][0],但是这题折磨了我5个月,我连r,v都用数组存了,这点花得起。 - cost[0][k]最好要初始化成inf。(不是一定要,但出了什么特殊情况我不负责)
随后,前步的费用加上后的费用就是步的费用。
cost[i][k]=cost[i][k-1]+cost[t[i][k-1]][k-1];(所以要先算To)
最后防溢出检测:(被折磨5个月不敢不谨慎)
if(cost[i][k]<0) cost[i][k]=inf;代码3
这次是真完结撒花了。
#include<iostream> #include<stack> #define nmax 200000 #define qmax 300000 #define lognmax 20 #define inf 0x7fffffff using namespace std; int d[nmax],c[nmax],r[qmax],v[qmax],t[nmax][lognmax],cost[nmax][lognmax]; int main(){ #ifdef local system(""); int logn=3; #endif //---输入O(n)---// #ifdef local cout<<"\033[32mn,q:\n\033[0m"; #endif int n,q; cin>>n>>q; #ifdef local cout<<"\033[32md,c:\n\033[0m"; #endif for(int i=1;i<=n;i++) cin>>d[i]>>c[i]; #ifdef local cout<<"\033[32mr,v:\n\033[0m"; #endif for(int i=1;i<=q;i++) cin>>r[i]>>v[i]; #ifdef local cout<<"\n"; #endif //---计算To数组O(logn)---// stack<int>mono; for(int i=1;i<=n;i++){ while(!mono.empty()&&d[mono.top()]<d[i]){ t[mono.top()][0]=i; mono.pop(); } mono.push(i); } for(int k=1;k<20;k++) for(int i=1;i<=n;i++) t[i][k]=t[t[i][k-1]][k-1]; #ifdef local cout<<"\033[32mTo数组:\n\033[0m"; for(int k=0;k<=logn;k++){ for(int i=1;i<=n;i++) cout<<t[i][k]<<" "; cout<<"\n"; } #endif //---计算Cost数组(logn)---// for(int i=1;i<=n;i++) cost[i][0]=c[i]; for(int k=0;k<20;k++) cost[0][k]=inf; for(int k=1;k<20;k++) for(int i=1;i<=n;i++){ cost[i][k]=cost[i][k-1]+cost[t[i][k-1]][k-1]; if(cost[i][k]<0) cost[i][k]=inf; } #ifdef local cout<<"\033[32mCost数组:\n\033[0m"; for(int k=0;k<=logn;k++){ for(int i=1;i<=n;i++) cout<<cost[i][k]<<" "; cout<<"\n"; } #endif //---解决并回答O(logn)---// #ifdef local cout<<"\033[32mans:\n\033[0m"; #endif for(int i=1;i<=q;i++){ for(int k=19;k>=0;k--) if(v[i]>cost[r[i]][k]){ v[i]-=cost[r[i]][k]; r[i]=t[r[i]][k]; } cout<<r[i]<<"\n"; } //---完结撒花---// return 0; }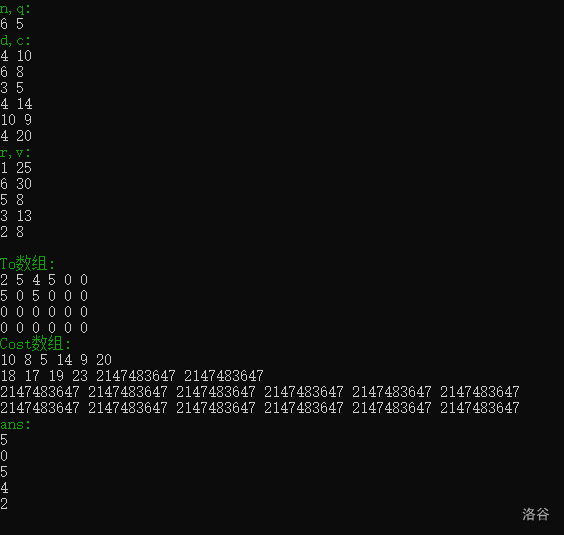
- 1
Information
- ID
- 271
- Time
- 1500ms
- Memory
- 512MiB
- Difficulty
- 9
- Tags
- # Submissions
- 30
- Accepted
- 2
- Uploaded By