3 solutions
-
3
有了这玩意,谁还用前缀和和差分啊!(仅限难题)
题意
不多赘述
思路
众所周知,前缀和和差分的功能是“互补”的。前缀和修改慢查询快,差分修改快查询慢。在学树状数组前可把
我同学们折磨坏了。而树状数组修改快查询也快,是个好东西。大概是这么存的:
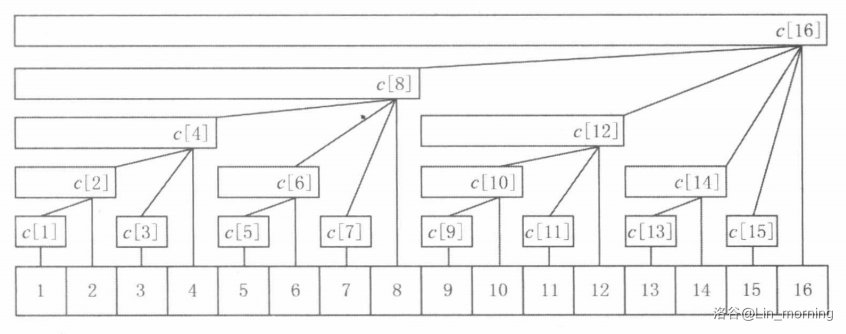
叶节点是原数组, 的长度代表它存哪几个点的值之和。
这一看就比前缀和好啊,就算修改第一个节点也只要 。查询最耗时也一样只需 。
不过从子节点跳到父节点看上去没规律啊。但你把它换成二进制就能发现: 的父节点是 [1];上一个兄弟节点是 [1:1]。
代码
#include <bits/stdc++.h> using namespace std; const int N = 5e5 + 5; int a[N],c[N]; int n,m; int lowbit(int x){ return x & -x; } void add(int i,int val){ for (;i <= n;i += lowbit(i)) c[i] += val; } int query(int r){ // [1,r] 之和 int res = 0; for (;r;r -= lowbit(r)) res += c[r]; return res; } int query(int l,int r){ // [l,r] 之和 return query(r) - query(l - 1); } int main(int argc, char **argv){ cin >> n >> m; for (int i = 1;i <= n;i++){ cin >> a[i]; add(i,a[i]); } while (m--){ int op,x,y; cin >> op >> x >> y; if (op == 1) add(x,y); else printf("%d\n",query(x,y)); } return 0; }
-
1
本题解供线段树使用
题意
维护一个单改区查,修改为加操作,查询为区间和。
思路
线段树单改区查,最重要的就是“四个函数”。
PushUp
目的
更新非叶子节点。
当子树有变动时要将新数据更新入父亲。
写法
取决于查询。本题目为求左右子树和。
不会没有人不知道线段树的左右节点是
2*i(i<<1)和2*i+1(i<<1|1)吧?void PushUp(int i){ tr[i]=tr[i<<1]+tr[i<<1|1]; }Build
目的
建树。
将叶子节点赋初值并沿路更新非叶子节点。
写法
递归分治。
- 边界情况:到达叶子节点,赋初值。l和r相等时l和r就是叶子节点在原数组的位置,所以有
tr[i]=a[l]。 - 一般情况:沿路更新。注意要等到递归完左右子树再更新。
- 递归条件:递归左右子树建树。
void Build(int i,int l,int r){ if(l==r){//叶子节点 tr[i]=a[l]; return; } //如果不是叶子节点: int mid=l+r>>1; Build(i<<1,l,mid);//递归处理 Build(i<<1|1,mid+1,r); PushUp(i);//最后沿路更新 }Update
目的
修改操作。
写法
取决于修改。这里为加上给定数。
先采用二分搜索找到所属节点,修改值后沿路更新。
void Update(int i,int l,int r,int x,int k){ if(l==r){//找到所属节点 tr[i]+=k; return;//这里视为边界处理 } int mid=l+r>>1; if(x<=mid)//二分思想 Update(i<<1,l,mid,x,k);//递归式二分 else Update(i<<1|1,mid+1,r,x,k); PushUp(i);//沿路更新 }Query
目的
查询操作。
写法
取决于查询。这里是加和。
比较难。(在单改区查线段树里面)
递归处理,对于一个节点:
- 被查询区间包含:直接返回节点值。
- 不被查询区间包含:依次判断左右子树与查询区间是否有重(chóng),有重则递归处理。最后把有效子树的返回合并返回。
- 附:在最后末尾节点区间长度为1,一定要么无重要么被包含,所以得证边界条件生效。
int Query(int i,int l,int r,int x,int y){ if(x<=l&&r<=y)//被包含。 return tr[i]; int mid=l+r>>1,ret=0; if(x<=mid)//左边有重,即查询左边界在左子树领域。 ret+=Query(i<<1,l,mid,x,y); if(mid<y)//右边有重,即查询右边界在右子树领域。 ret+=Query(i<<1|1,mid+1,r,x,y); return ret; //因为没有值被修改,所以不用PushUp。 }代码
#include<iostream> #define N int(6e5) using namespace std; int n=0,a[N]{},tr[4*N]{};//学过线段树都知道要开4倍空间。 void PushUp(int i){ tr[i]=tr[i<<1]+tr[i<<1|1]; } void Build(int i,int l,int r){ if(l==r){//叶子节点 tr[i]=a[l]; return; } //如果不是叶子节点: int mid=l+r>>1; Build(i<<1,l,mid);//递归处理 Build(i<<1|1,mid+1,r); PushUp(i);//最后沿路更新。 } void Update(int i,int l,int r,int x,int k){ if(l==r){//找到所属节点 tr[i]+=k; return;//这里视为边界处理 } int mid=l+r>>1; if(x<=mid)//二分思想 Update(i<<1,l,mid,x,k);//递归式二分 else Update(i<<1|1,mid+1,r,x,k); PushUp(i);//沿路更新 } int Query(int i,int l,int r,int x,int y){ if(x<=l&&r<=y)//被包含。 return tr[i]; int mid=l+r>>1,ret=0; if(x<=mid)//左边有重,即查询左边界在左子树领域。 ret+=Query(i<<1,l,mid,x,y); if(mid<y)//右边有重,即查询右边界在右子树领域。 ret+=Query(i<<1|1,mid+1,r,x,y); return ret; //因为没有值被修改,所以不用PushUp。 } int main(){ int m=0; cin>>n>>m; for(int i=1;i<=n;i++) cin>>a[i]; Build(1,1,n); while(m--){ int op=0;//操作类型 cin>>op; if(op==1){ int x=0,k=0; cin>>x>>k; Update(1,1,n,x,k); } if(op==2){ int x=0,y=0; cin>>x>>y; cout<<Query(1,1,n,x,y)<<"\n"; } } return 0; }tips
主要难点:
- 理解PushUp。
- Query函数。
另外C23lvzekai的题解里面使用了
#define int long long,这是没有必要的,因为题目说的是区间和为,但是如果说的是元素为,就有可能爆int。 - 边界情况:到达叶子节点,赋初值。l和r相等时l和r就是叶子节点在原数组的位置,所以有
-
-2
- 1
Information
- ID
- 274
- Time
- 1000ms
- Memory
- 512MiB
- Difficulty
- 7
- Tags
- # Submissions
- 83
- Accepted
- 16
- Uploaded By
