题意

求用1*2的长方形填充n*m的长方形有多少种情况。

思路

一眼小奥(bushi)。

n=2就是肥婆辣鸡数列，n=3就是，就是，就是布吉岛。

先想想n=2的时候是怎么推的。

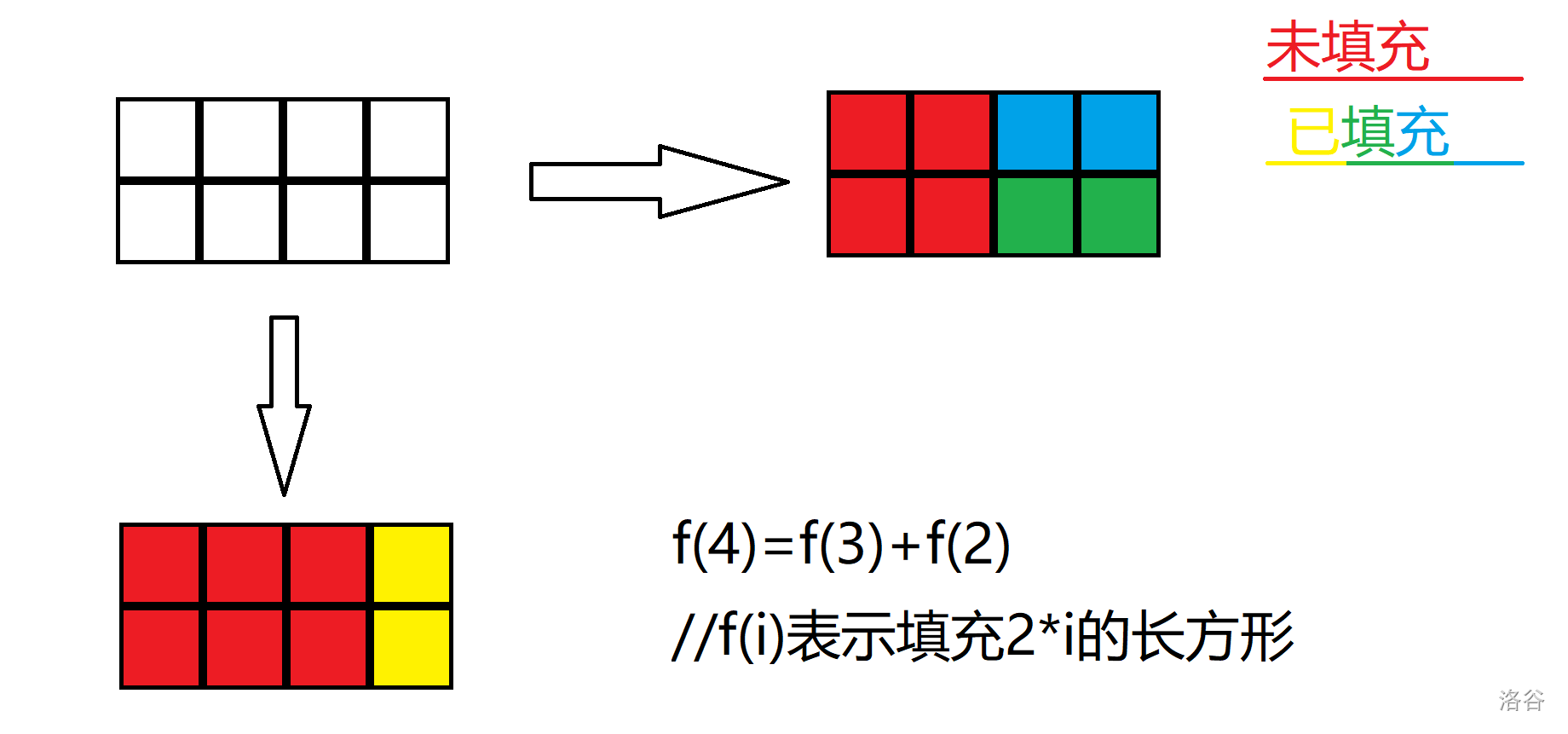
所以以此类推，确定中心思想：

固定一边长，推另一边长。

所以我们可以把一整行当作状态。

什么？开11维数组？那、很、麻、烦、了。所以我选：

状态压缩！

0/1是什么意思？

1表示这一位有向下插的长方形。

f[i][j]表示第j行状态为i能被什么玩意推过来。

所以上一行的1就是这一行被插的。

f[x][i-1]|f[y][i]就能得到这一行已经被填充的。（向下插或者被上面的插）好像什么不对？

那么剩下的0就只能两两抱团取暖（打横）。更不对了？

所以我们可以得到一个结论，如果f[x][i-1]|f[y][i]有连续奇数0，就不可行。

bool iscan(long long x,long long n){
    long long cnt=0;
    for(long long i=0;i<n;i++){
        if(x>>i&1){
            if(cnt&1) 
				return false;
            cnt=0;
        }
        else
			cnt++;
    }
    return !(cnt&1);
}

因为每次都iscan太麻烦了，先打个表：

	for(long long i=0;i<10000;i++)
		for(long long j=0;j<15;j++)
			f[i][j]=0;

tips：注意m的大小会影响边界0的奇偶，所以每一次测试都要重新打表。

然后状压经典暴枚：

for(long long i=1;i<=n;i++)
		for(long long x=0;x<(1<<m);x++)
			for(long long y=0;y<(1<<m);y++)
				if(!(x&y)&can[x|y])
					f[y][i]+=f[x][i-1];

然后，然后就没有了呀……

代码

#include<iostream>
using namespace std;
long long f[10000][15];
bool can[10000];
int main();
void Hmain(long long,long long);
bool iscan(long long,long long);
int main(){
	while(true){
		long long h,w;
		cin>>h>>w;
		if(h==0||w==0)
			return 0;
		Hmain(h,w);
	}
	return 0;
}
void Hmain(long long n,long long m){
	for(long long i=0;i<(1<<m);i++)
		can[i]=iscan(i,m);
	for(long long i=0;i<10000;i++)
		for(long long j=0;j<15;j++)
			f[i][j]=0;
	f[0][0]=1;
	for(long long i=1;i<=n;i++)
		for(long long x=0;x<(1<<m);x++)
			for(long long y=0;y<(1<<m);y++)
				if(!(x&y)&can[x|y])
					f[y][i]+=f[x][i-1];
	cout<<f[0][n]<<"\n";
}
bool iscan(long long x,long long n){
    long long cnt=0;
    for(long long i=0;i<n;i++){
        if(x>>i&1){
            if(cnt&1) 
				return false;
            cnt=0;
        }
        else
			cnt++;
    }
    return !(cnt&1);
}