思路

由于只能由 1x2 的长方形组成，所以 $hw$ 为奇数的情况直接特判。

主体是hyr的思路（状态压缩部分），我讲讲奇偶性的判断。

首先，定义一下状态意思：

• 0 代表一个横半格或竖半格的下半格。
• 1 代表一个竖半格的上半格。

例子（灰色是竖格）：

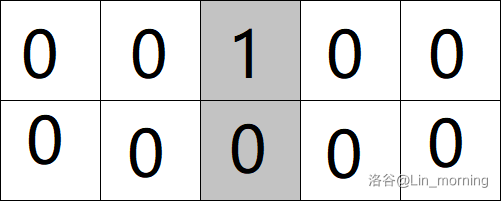
回到方格，我们有一个想法：如果一行内有连续奇数个空格，会不会不合法（导致没有方案）。

结合状态意义，有人会说：如果是奇数个 0 的话，让上一行来个竖格不就行了吗。

但请大家在脑海里想想再下面的情况 （绝对不是因为我懒得画图了） ，可以发现是无限循环（可以以宽度为 3 来想）。

（大概是这样，数字区分不同的方块，0 代表没有方块）

010
212
202

如表，所以可以证明一行内有连续奇数个空格是不合法的。

结合状态意义，可以发现，当前行或（|）上上一行就能得出当前行的情况了。

最后总结：

1. 如何状态压缩（见hyr题解，本文略）
2. 奇偶性判断（本文主要内容）
3. 记得状态不要冲突（不能有两个相同位置的 1）

代码

hyr的代码感觉好乱啊

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 15,M = 1 << 12;
int n,m;
ll dp[N][M];
bool check(int x){// 检查奇偶性
	int cnt = 0;
	x |= 1 << m;
	while (x){
		if (x & 1){
			if (cnt & 1)	return 0;
			cnt = 0;
		}else	cnt++;
		x >>= 1;
	}
	return 1;
}
int main(int argc, char **argv){
	cin >> n >> m;
	while (n || m){
		if (n * m & 1){// 特判
			cout << "0\n";
			cin >> n >> m;
			continue;
		}
		memset(dp,0,sizeof dp);
		
		for (int i = 0;i < 1 << m;i++){// 第一行不用考虑竖半格的下半格
			if (check(i))	dp[1][i] = 1;
		}
		for (int i = 2;i <= n;i++){
			for (int j1 = 0;j1 < 1 << m;j1++){	// 当前行
				for (int j2 = 0;j2 < 1 << m;j2++){	// 上一行
					if (j1 & j2 || // 检查竖半格冲突
						!check(j1 | j2))	continue;
					dp[i][j1] += dp[i - 1][j2];
				}
			}
		}
		cout << dp[n][0] << '\n';
		cin >> n >> m;
	}
	return 0;
}

记忆化搜索

思路见HYR的

#include<bits/stdc++.h>
using namespace std;
long long f[12][1<<11];
long long h,w;
bool check(long long pp){
	long long cnt=0;
	for(int i=0;i<w;i++)
		if(pp&(1<<i))
			if(cnt&1)return false;
			else cnt=0;
		else cnt++;
	return (cnt&1)==0;
}
long long dp(long long d,long long pp){
	if(d==0)return pp==0;
	if(f[d][pp]!=-1)return f[d][pp];
	long long ans=0;
	for(int i=0;i<(1<<w);i++)
		if((i&pp)==0&&check(i|pp))
			ans+=dp(d-1,i);
	return f[d][pp]=ans;
}
int main(){
	while(cin>>h>>w){
		if(h==0&&w==0)break;
		memset(f,-1,sizeof f);
		cout<<dp(h,0)<<endl;
	}
}

题意

求用1*2的长方形填充n*m的长方形有多少种情况。

思路

一眼小奥(bushi)。

n=2就是肥婆辣鸡数列，n=3就是，就是，就是布吉岛。

先想想n=2的时候是怎么推的。

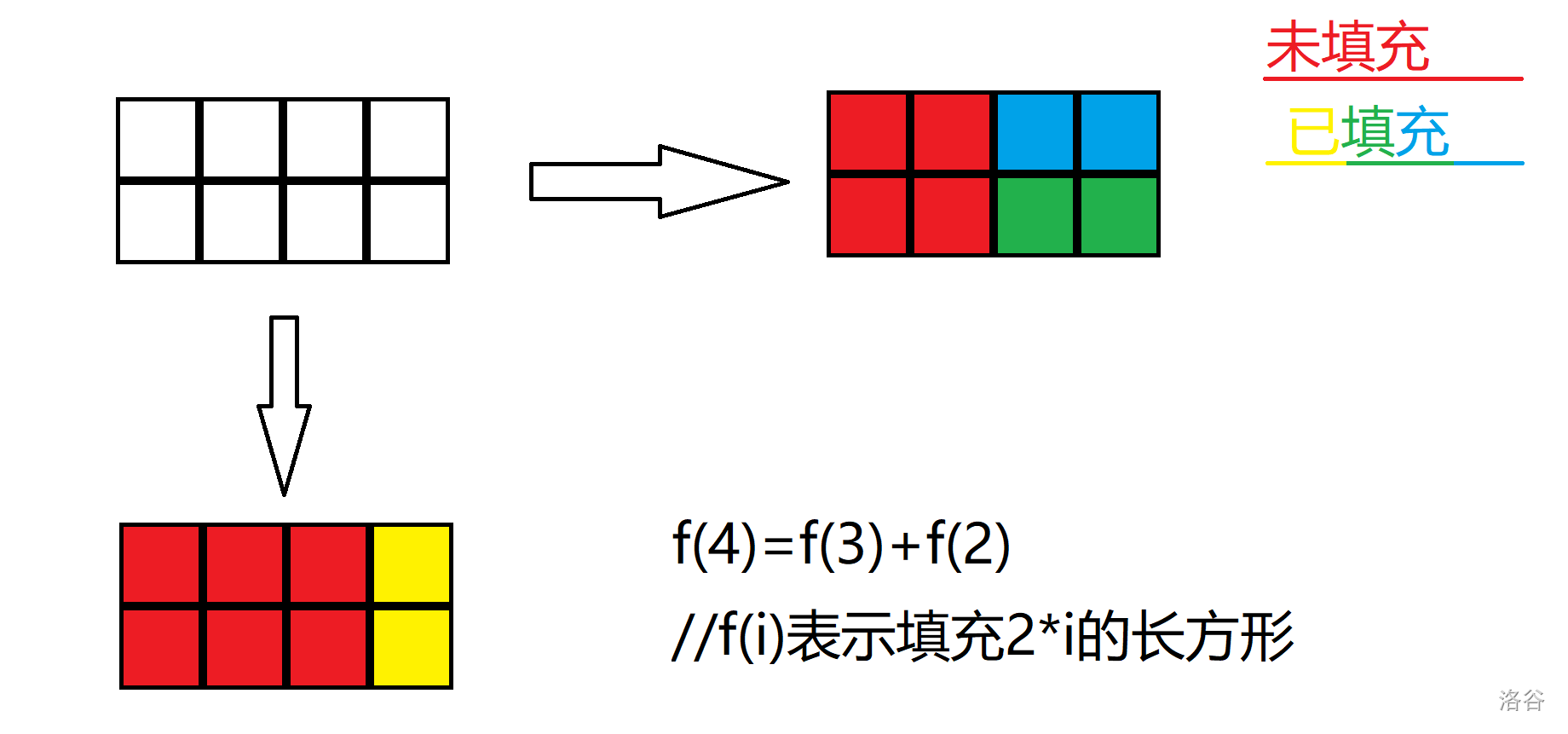
所以以此类推，确定中心思想：

固定一边长，推另一边长。

所以我们可以把一整行当作状态。

什么？开11维数组？那、很、麻、烦、了。所以我选：

状态压缩！

0/1是什么意思？

1表示这一位有向下插的长方形。

f[i][j]表示第j行状态为i能被什么玩意推过来。

所以上一行的1就是这一行被插的。

f[x][i-1]|f[y][i]就能得到这一行已经被填充的。（向下插或者被上面的插）好像什么不对？

那么剩下的0就只能两两抱团取暖（打横）。更不对了？

所以我们可以得到一个结论，如果f[x][i-1]|f[y][i]有连续奇数0，就不可行。

bool iscan(long long x,long long n){
    long long cnt=0;
    for(long long i=0;i<n;i++){
        if(x>>i&1){
            if(cnt&1) 
				return false;
            cnt=0;
        }
        else
			cnt++;
    }
    return !(cnt&1);
}

因为每次都iscan太麻烦了，先打个表：

	for(long long i=0;i<10000;i++)
		for(long long j=0;j<15;j++)
			f[i][j]=0;

tips：注意m的大小会影响边界0的奇偶，所以每一次测试都要重新打表。

然后状压经典暴枚：

for(long long i=1;i<=n;i++)
		for(long long x=0;x<(1<<m);x++)
			for(long long y=0;y<(1<<m);y++)
				if(!(x&y)&can[x|y])
					f[y][i]+=f[x][i-1];

然后，然后就没有了呀……

代码

#include<iostream>
using namespace std;
long long f[10000][15];
bool can[10000];
int main();
void Hmain(long long,long long);
bool iscan(long long,long long);
int main(){
	while(true){
		long long h,w;
		cin>>h>>w;
		if(h==0||w==0)
			return 0;
		Hmain(h,w);
	}
	return 0;
}
void Hmain(long long n,long long m){
	for(long long i=0;i<(1<<m);i++)
		can[i]=iscan(i,m);
	for(long long i=0;i<10000;i++)
		for(long long j=0;j<15;j++)
			f[i][j]=0;
	f[0][0]=1;
	for(long long i=1;i<=n;i++)
		for(long long x=0;x<(1<<m);x++)
			for(long long y=0;y<(1<<m);y++)
				if(!(x&y)&can[x|y])
					f[y][i]+=f[x][i-1];
	cout<<f[0][n]<<"\n";
}
bool iscan(long long x,long long n){
    long long cnt=0;
    for(long long i=0;i<n;i++){
        if(x>>i&1){
            if(cnt&1) 
				return false;
            cnt=0;
        }
        else
			cnt++;
    }
    return !(cnt&1);
}