5 solutions

  • 10
    @ 2024-4-24 13:29:00

    优质bellman_ford,spfa题解(HMZ发布)

    题意

    求一个图的某一个点到其他所有点的最短路长度

    思路

    存储

    不可以用邻接矩阵,因为n≤104n≤10^4,可能会MLEMLE

    我的做法是邻接表

    dijkstra(普通版)

    参考 OI WiKi - dijkstra

    对于每个点,分两步

    • 求出整个图中最短路长度最短的点
    • 将这个点所有连接的边标记为最短的长度[1]

    直到没有最短路可更新

    dijkstra(优化版)

    "求出整个图中最短路长度最短的点"这一段话是指目前已探索的点的最短路径最小的点

    不如使用优先队列优化

    对于每个点,分两步

    • 获取队列顶的点
    • 弹出
    • 将这个点所有连接的边标记为最短的长度
    • 将这个点如队列

    直到队列没有元素

    tips:

    • 因为优先队列是从大到小,所以要调整

      priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >q;

    如果你记不住,也许你可以这样想

    将距离改为相反数再入队列

    优先队列

    与普通队列不同的是可以排序数据,从大到小!!!

    可以

    • push() 推入元素
    • pop() 弹出元素
    • top() 返回队列的顶部
    • size() 返回队列长度

    数据

    1≤n≤104,1≤m≤5×105,w>0,∑w<2311≤n≤10^4,1≤m≤5×10^5,w>0,∑w<2^{31}

    2147483647=231−12147483647=2^{31}-1

    代码(普通版)

    #include<iostream>
#include<vector>
#define INF 2147483647
#define N 11451
using namespace std;
int n,m,s;
struct node
{
    int v,l;//下一个点,边权
};
vector<node>g[N];//图
int len[N]={0};//记录最短路
int vis[N]={0};//标记数组
void dijkstra()
{
	for(int i=1;i<=n;i++)
	{
		int u=-1,mi=INF;//初始值注意!
		for(int j=1;j<=n;j++)
		{
			if(!vis[j] && len[j]<mi)//最短路最短的点
			{
				u=j;//记录
				mi=len[j];
			}
		}
		if(u==-1)//没有可以更新的点
		{
			return;
		}
		vis[u]=1;//标记
		for(int j=0;j<g[u].size();j++)//每下一个点
		{
			int v=g[u][j].v;
			if((!vis[v]) && len[u]+g[u][j].l<len[v])//发现有更短的路
			{
				len[v]=len[u]+g[u][j].l;//更新
			}
		}
	}
}
int main()
{
	fill(len,len+N,INF);//全部设为INF(2147483647)
    cin>>n>>m>>s;//输入
    len[s]=0;//初始距离
    for(int i=0;i<m;i++)
    {
        int u,v,w;
        cin>>u>>v>>w;//输入
        g[u].push_back({v,w});//添加边
    }
    dijkstra();
    for(int i=1;i<=n;i++)
    {
    	cout<<len[i]<<" ";//输出
	}
    return 0;//完结散花
}

    代码(优化版)

    #include<bits/stdc++.h>
#define INF 2147483647
#define N 114514
using namespace std;
int n,m,s;
struct node
{
    int v,w;
};
vector<node>g[N];
int d[N];
int vis[N];
priority_queue<pair<int,int> >q;//使用队列优化
void dijkstra()
{
    while(q.size())//注意这里
    {
        int u=q.top().second;//取出队列顶
        q.pop();//出队列
        vis[u]=1;//标记
        for(int j=0;j<g[u].size();j++)
        {
            int v=g[u][j].v;
            int w=g[u][j].w;
            if(d[u]+w<d[v])
            {
                d[v]=d[u]+w;//更新
                q.push({-d[v],v});//入队列
            }
        }
    }
}
int main()
{
    cin>>n>>m>>s;
    for(int i=0;i<m;i++)
    {
        int u,v,w;
        cin>>u>>v>>w;
        g[u].push_back({v,w});
        d[u]=INF;
        d[v]=INF;
    }
    d[s]=0;
    q.push({-d[s],s});//初始值
    dijkstra();
    for(int i=1;i<=n;i++)
    {
        cout<<d[i]<<" ";
    }
    return 0;
}

    1. 指这个点最短路加上边权使得与连接的那个点标记的最短路更短,就更新最短路 ↩︎

    • @ 2024-4-26 20:59:11

      优质题解，点赞👍

      倡导大家都发这样的优质题解，不要发列支体节

    • @ 2024-4-27 15:57:24

      @ 你打广告的时候想到这点了吗？

    • @ 2024-4-28 19:43:51

      @列支体节

    • @ 2024-5-24 17:52:36

      @

      你他妈！

      我踏马什么时候发过广告！

      发广告的使我们这边的 @ 你踏马开喷前能不能看一下人名？

      他是天河校区初一五班潘伟明，我是天河校区初一一班黄煜然，你********

    • @ 2024-5-24 17:55:03

      @

      你看他用户名都能看出来他是个广告狂，甚至用户名都是广告！你他妈，别冤枉人！

  • 5
    @ 2024-4-30 19:56:52

    不会链式前向星的看这里

    BF

    BF 是 Dijkstra 的老祖宗。

    BF 就是暴力搜所有边，找出最短路径树

    BF 用到了三角不等式，就是说如果 dis[v]<=dis[u]+wu,vdis[v] <= dis[u] + w_{u,v}，那么 dis 存的就是起点到 v 的最短距离。例子：

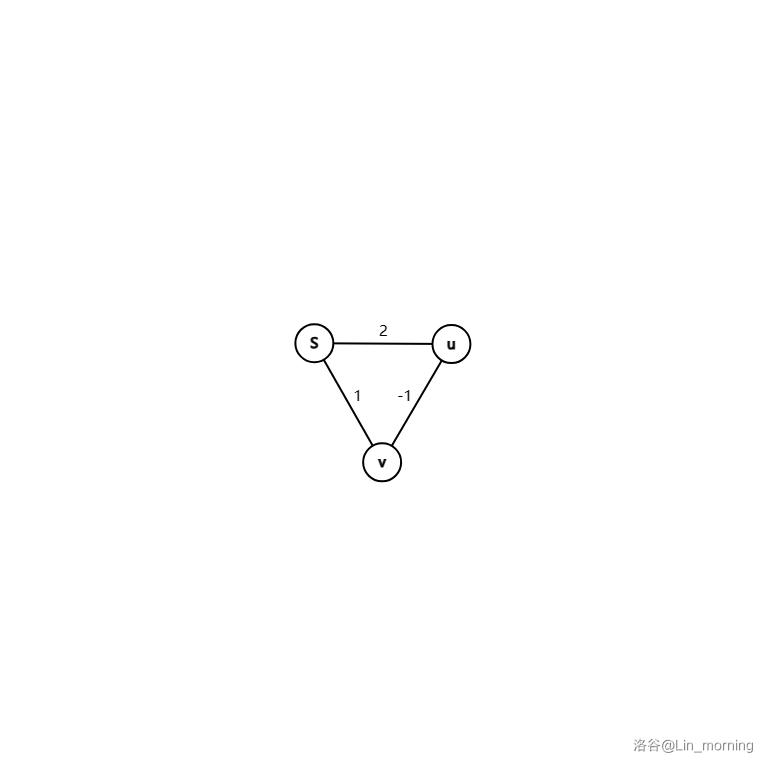
    SPFA 是 BF 的队列优化，自行理解

    代码（BF）

    #include <bits/stdc++.h>
using namespace std;
const int N = 10005,M = 500005,INF = 1073741823;

// 链式前向星
struct edge{
	int u,v,w,prev;
}edges[M];
int tail[N],tot;
void add_edge(int u,int v,int w){
	edges[++tot] = {u,v,w,NULL};
	edges[tot].prev = tail[u];
	tail[u] = tot;
}

int dis[N],n,m,s;
void bf(){
	for (int i = 1;i < n;i++){
		bool f = 1;
		for (int j = 1;j <= m;j++){	// 注意：要遍历所有边，而不只是临边
			int u = edges[j].u,v = edges[j].v,w = edges[j].w;
			if (dis[u] + w < dis[v]){
				dis[v] = dis[u] + w;
				f = 0;
			}
		}
		if (f)	return;	// 所有边都满足了三角不等式，直接退出
	}
}
int main(int argc, char **argv){
	fill(dis,dis + N,INF);
	cin >> n >> m >> s;
	dis[s] = 0;
	for (int i = 0;i < m;i++){
		int u,v,w;
		cin >> u >> v >> w;
		add_edge(u,v,w);
	}
	bf();
	for (int i = 1;i <= n;i++){
		if (dis[i] == INF)	printf("%d ",0x7fffffff);
		else	printf("%d ",dis[i]);
	}
	return 0;
}

    代码（SPFA）

    #include <bits/stdc++.h>
using namespace std;
const int N = 10005,M = 500005,INF = 1073741823;

// 链式前向星
struct edge{
	int u,v,w,prev;
}edges[M];
int tail[N],tot;
void add_edge(int u,int v,int w){
	edges[++tot] = {u,v,w,tail[u]};
	tail[u] = tot;
}

int dis[N],n,m,s;
bool f[N];
void bf(){
	queue<int> q;
	q.push(s);
	while (!q.empty()){
		int u = q.front();
		q.pop();
		f[u] = 0;
		for (int j = tail[u];j;j = edges[j].prev){
			int v = edges[j].v,w = edges[j].w;
			if (dis[u] + w < dis[v]){
				dis[v] = dis[u] + w;
				if (!f[v])	q.push(v),f[v] = 1;
			}
		}
	}
}
int main(int argc, char **argv){
	fill(dis,dis + N,INF);
	cin >> n >> m >> s;
	dis[s] = 0;
	for (int i = 0;i < m;i++){
		int u,v,w;
		cin >> u >> v >> w;
		add_edge(u,v,w);
	}
	bf();
	for (int i = 1;i <= n;i++){
		if (dis[i] == INF)	printf("%d ",0x7fffffff);
		else	printf("%d ",dis[i]);
	}
	return 0;
}
  • 5
    @ 2024-4-28 12:57:17

    本题解在 @ 的这篇题解的基础上将 vector 换成了链式前向星[1]。

    代码（Dijkstra）

    #include <bits/stdc++.h>
using namespace std;
// 注意 INF 要设成 2^30-1，否则会爆成负数
const int N = 10005,M = 500005,INF = 1073741823;

// 链式前向星
struct edge{
	int v,w,prev;
	// v：目标点
	// w：边权
	// prev：上一个点
}edges[M];	// 数组存链表
int tail[N],tot;
// tail：指向 i 能到的点的链表的末尾
// tot：edges 最后一个点的下标
void add_edge(int u,int v,int w){
	edges[++tot] = {v,w,NULL};
	edges[tot].prev = tail[u];
	tail[u] = tot;
}

int dis[N],n,m,s;
bool f[N];
void dkstr(){
	for (int i = 1;i <= n;i++){
		int u = -1,mn = INF;
		for (int j = 1;j <= n;j++){
			if (!f[j] && dis[j] < mn){
				u = j;
				mn = dis[j];
			}
		}
		if (u == -1)	return ;
		f[u] = 1;
		for (int j = tail[u];j;j = edges[j].prev){
			int v = edges[j].v,w = edges[j].w;
			if (!f[v])	dis[v] = min(dis[v],dis[u] + w);
		}
	}
}
int main(int argc, char **argv){
	fill(dis,dis + N,INF);
	cin >> n >> m >> s;
	dis[s] = 0;
	for (int i = 0;i < m;i++){
		int u,v,w;
		cin >> u >> v >> w;
		add_edge(u,v,w);
	}
	dkstr();
	for (int i = 1;i <= n;i++){
		if (dis[i] == INF)	printf("%d ",0x7fffffff);
		else	printf("%d ",dis[i]);
	}
	return 0;
}

    1. 链式前向星 ↩︎

    • 3
      @ 2024-4-30 19:25:45 
      #include<bits/stdc++.h> 
using namespace std;
struct str{
	int u,v,w;
};
str g[1000001];
long long dis[1000001];
int main(){
	int n,m,s;
	cin>>n>>m>>s;
	memset(dis,0x3f,sizeof dis);
	dis[s]=0;
	for(int i=1;i<=m;i++){
		cin>>g[i].u>>g[i].v>>g[i].w;
	}
	for(int i=1;i<n;i++){
		bool f=0;
		for(int j=1;j<=m;j++){
			long long u2=g[j].u;
			long long v2=g[j].v;
			long long w2=g[j].w;
			if(dis[v2]>dis[u2]+w2){
				dis[v2]=dis[u2]+w2;
				f=1;
			}
		} 
		if(f==0){
			break;
		}
	}
	for(int i=1;i<=n;i++){
		if(dis[i]==0x3f3f3f3f3f3f3f3f){
			cout<<2147483647<<" ";
			continue;
		}
		else{
			cout<<dis[i]<<" ";
		}
	}
}
      • -11
        @ 2024-4-27 16:07:53

        无注释题解

        #include<iostream>
#include<vector>
#define INF 2147483647
#define N 11451
using namespace std;
int n,m,s;
struct node
{
    int v,l;
};
vector<node>g[N];
int len[N] = {0}; 
int vis[N] = {0};
void dijkstra()
{
	for(int i = 1;i <= n;i++)
	{
		int u = -1,mi = INF;
		for(int j = 1;j <= n;j++)
		{
			if(!vis[j] && len[j] < mi)
			{
				u = j;
				mi = len[j];
			}
		}
		if(u == -1)
		{
			return;
		}
		vis[u] = 1;
		for(int j = 0;j < g[u].size();j++)
		{
			int v = g[u][j].v;
			if((!vis[v]) && len[u] + g[u][j].l < len[v])
			{
				len[v] = len[u] + g[u][j].l;
			}
		}
	}
}
int main()
{
	fill(len,len + N,INF);
    cin >> n >> m >> s;
    len[s] = 0;
    for(int i = 0;i < m;i++)
    {
        int u,v,w;
        cin >> u >> v >> w;
        g[u].push_back({v,w});
    }
    dijkstra();
    for(int i = 1;i <= n;i++)
    {
    	cout << len[i] << " ";
	}
    return 0;
}
        • @ 2024-4-28 18:21:08

          和PWM的基本一样耶😕

      • 1

      【模板】单源最短路径（弱化版）

      Information

      ID
      1065
      Time
      1000ms
      Memory
      125MiB
      Difficulty
      8
      Tags
      # Submissions
      225
      Accepted
      35
      Uploaded By
      1. About
      2. Contact Us
      3. Privacy
      4. Terms of Service
      5. Copyright Complaint
      6. Language
      7. Legacy mode
      8. Theme
      2. 粤ICP备2022044963号-1
      3. Worker 0, 29ms
      4. Powered by Hydro v4.13.3 Community