必看卡特兰数递推公式详细推导过程

一、卡特兰数的公式

卡特兰数的公式为：

$C_n = \frac{1}{n+1} \binom{2n}{n}$

注：其中组合数$\binom{2n}{n}$表示从 $2n$ 个元素中选 $n$ 个的方案总数

推导过程请见: "三、证明卡兰特公式"

二、公式推导 (个人过程)

1. 表达比值：

$\frac{C_n}{C_{n-1}} = \frac{\frac{1}{n+1} C_{2n}^{n}}{\frac{1}{n} C_{2n-2}^{n-1}}$

2. 展开：

$C_{2n}^{n} = \frac{(2n)!}{n!n!}, \quad C_{2n-2}^{n-1} = \frac{(2n-2)!}{(n-1)!(n-1)!}$

2.2 代入比值：

$\frac{C_n}{C_{n-1}} = \frac{\frac{1}{n+1} \cdot \frac{(2n)!}{n!n!}}{\frac{1}{n} \cdot \frac{(2n-2)!}{(n-1)!(n-1)!}} = \frac{n}{n+1} \cdot \frac{(2n)(2n-1)}{n^2}$

这一段手打有亿点点难 点个赞吧

3. 化简：

$\frac{(2n)!}{(2n-2)!} = (2n)(2n-1), \quad \frac{(n-1)!}{n!} = \frac{1}{n}$

继续：

$\frac{C_n}{C_{n-1}} = \frac{n}{n+1} \cdot \frac{2(2n-1)}{n} = \frac{4n-2}{n+1}$

4. 得到公式：

$C_n = \frac{4n-2}{n+1} C_{n-1}$

三、证明卡兰特公式

结论：

$C_{2n}^{n} - C_{2n}^{n-1} = \frac{1}{n+1}C_{2n}^{n}$，

即：

$C_{2n}^{n} - C_{2n}^{n-1} = \frac{C_{2n}^{n}}{n+1}$

如图

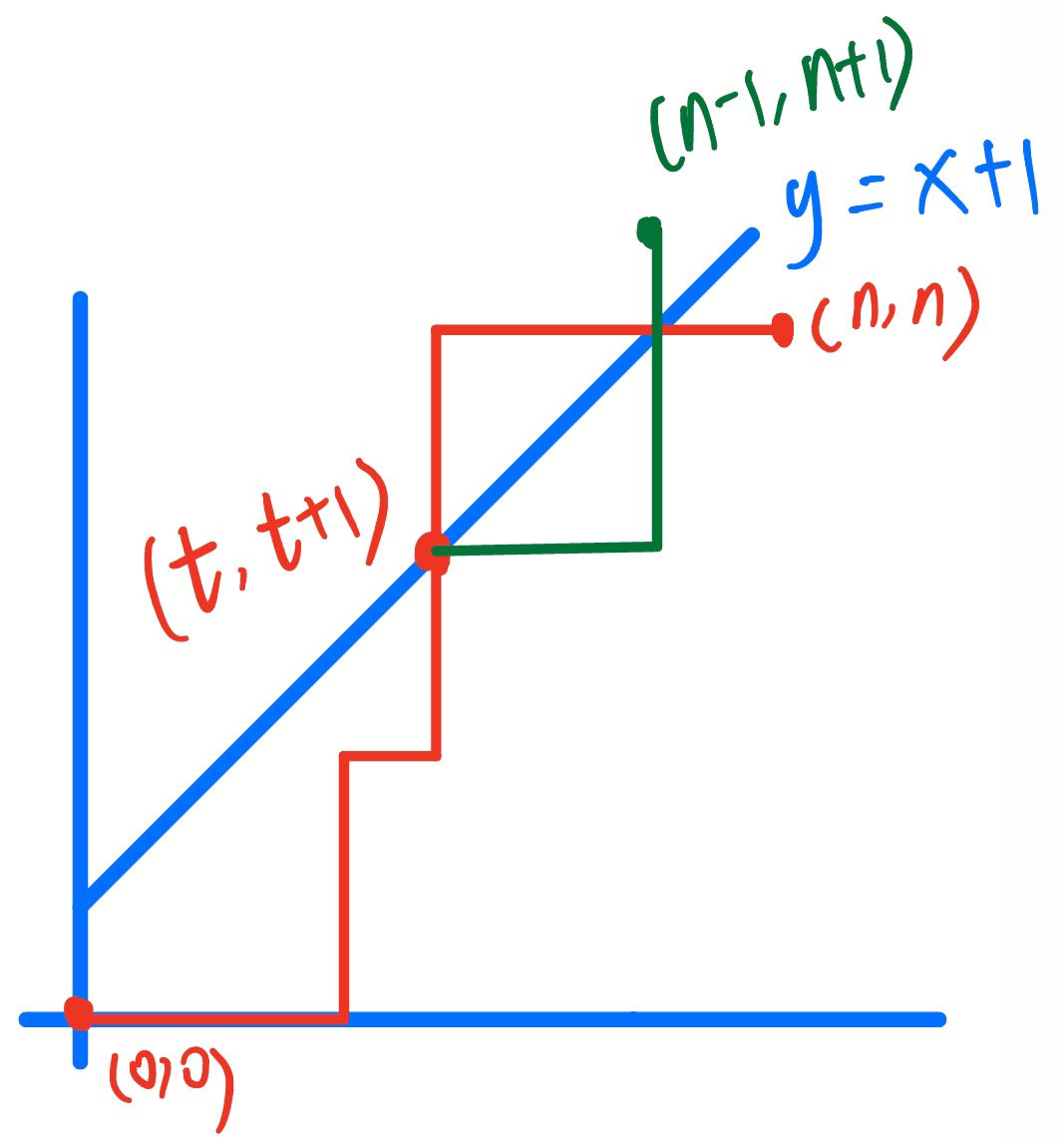
红色为不合法的路径,绿色为做完对称的路径

1. 展开：

$C_{2n}^{n} - C_{2n}^{n-1} = \frac{(2n)!}{n!n!} - \frac{(2n)!}{(n-1)!(n+1)!}$

2. 通分：

$\frac{(2n)! (n+1 - n)}{n!(n+1)!} = \frac{(2n)!}{n!(n+1)!} = \frac{1}{n+1} C_{2n}^{n}$

意义： 合路线总数-非法路径数=合法路径数，等于 $C_{2n}^{n} - C_{2n}^{n-1}$

看懂请留下点赞 谢谢！