题目描述

If we define $f(0) = 1, f(1) = 0, f(4) = 1, f(8) = 2, f(16) = 1, \dots$, do you know what function $f$ means?

Actually, $f(x)$ calculates the total number of enclosed areas produced by each digit in $x$. The following table shows the number of enclosed areas produced by each digit:

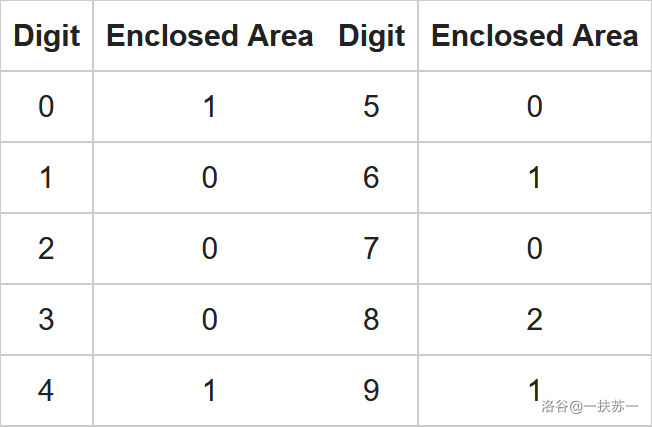
For example, $f(1234) = 0 + 0 + 0 + 1 = 1$, and $f(5678) = 0 + 1 + 0 + 2 = 3$.

We now define a recursive function $g$ by the following equations:

$$\begin{cases} g^0(x) = x \\ g^k(x) = f(g^{k-1}(x)) & \text{if } k \ge 1 \end{cases} $$

For example, $g^2(1234) = f(f(1234)) = f(1) = 0$, and $g^2(5678) = f(f(5678)) = f(3) = 0$.

Given two integers $x$ and $k$, please calculate the value of $g^k(x)$.

输入格式

There are multiple test cases. The first line of the input contains an integer $T$ (about $10^5$), indicating the number of test cases. For each test case:

The first and only line contains two integers $x$ and $k$ ($0 \le x, k \le 10^9$). Positive integers are given without leading zeros, and zero is given with exactly one `0'.

输出格式

For each test case output one line containing one integer, indicating the value of $g^k(x)$.

6
123456789 1
888888888 1
888888888 2
888888888 999999999
98640 12345
1000000000 0

5
18
2
0
0
1000000000

提示