题目描述

Given an undirected simple graph with $n$ ($n \ge 3$) vertices and $m$ edges where the vertices are numbered from 1 to $n$, we call it a sub-cycle graph if it's possible to add a non-negative number of edges to it and turn the graph into exactly one simple cycle of $n$ vertices.

Given two integers $n$ and $m$, your task is to calculate the number of different sub-cycle graphs with $n$ vertices and $m$ edges. As the answer may be quite large, please output the answer modulo $10^9+7$.

Recall that

• A simple graph is a graph with no self loops or multiple edges;
• A simple cycle of $n$ ($n \ge 3$) vertices is a connected undirected simple graph with $n$ vertices and $n$ edges, where the degree of each vertex equals to 2;
• Two undirected simple graphs with $n$ vertices and $m$ edges are different, if they have different sets of edges;
• Let $u < v$, we denote $(u, v)$ as an undirected edge connecting vertices $u$ and $v$. Two undirected edges $(u_1, v_1)$ and $(u_2, v_2)$ are different, if $u_1 \ne u_2$ or $v_1 \ne v_2$.

输入格式

There are multiple test cases. The first line of the input contains an integer $T$ (about $2 \times 10^4$), indicating the number of test cases. For each test case:

The first and only line contains two integers $n$ and $m$ ($3 \le n \le 10^5$, $0 \le m \le \frac{n(n-1)}{2}$), indicating the number of vertices and the number of edges in the graph.

It's guaranteed that the sum of $n$ in all test cases will not exceed $3 \times 10^7$.

输出格式

For each test case output one line containing one integer, indicating the number of different sub-cycle graphs with $n$ vertices and $m$ edges modulo $10^9+7$.

3
4 2
4 3
5 3

15
12
90

提示

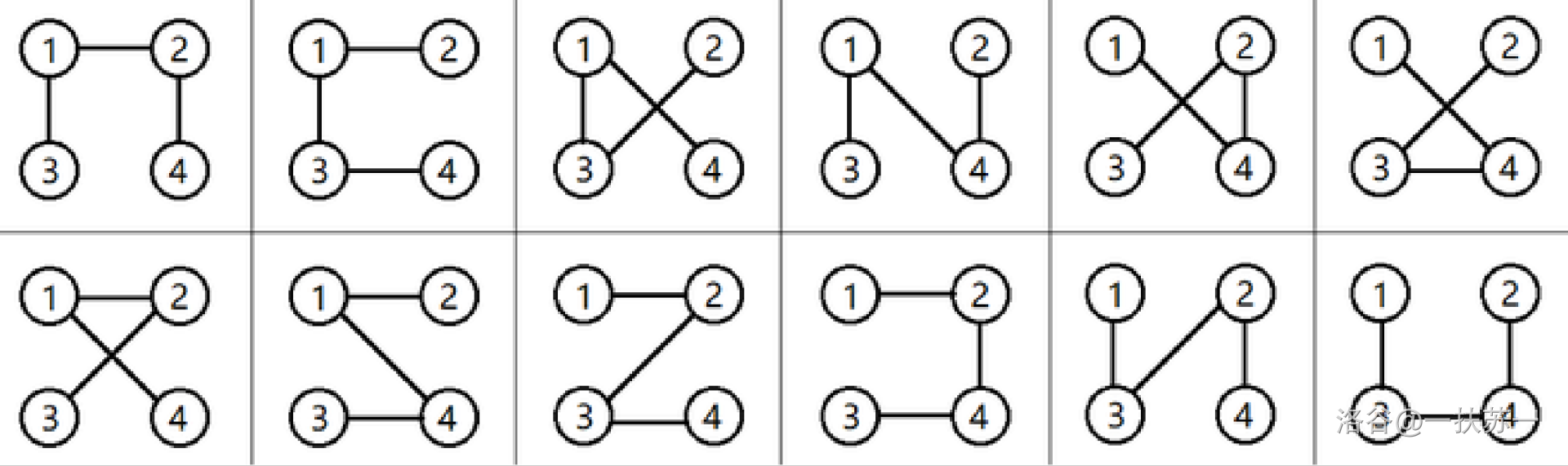
The 12 sub-cycle graphs of the second sample test case are illustrated below.