#P9895. [ICPC 2018 Qingdao R] Airdrop
[ICPC 2018 Qingdao R] Airdrop
题目描述
PUBG is a multiplayer online battle royale video game. In the game, up to one hundred players parachute onto an island and scavenge for weapons and equipment to kill others while avoiding getting killed themselves. Airdrop in this game is a key element, as airdrops often carry with them strong weapons or numerous supplies, helping players to survive.
 textit{Airdrop in the game(?)
textit{Airdrop in the game(?)
Consider the battle field of the game to be a two-dimensional plane. An airdrop has just landed at point (both and are integers), and all the players on the battle field, where (both and are integers) indicates the initial position of the -th player, start moving towards the airdrop with the following pattern:
- If the position of a living player at the beginning of this time unit is not equal to , he will begin his next move.
-
- Let's say he is currently at point . For his next move, he will consider four points , , and .
-
- He will select one of the four points whose Manhattan distance to the airdrop is the smallest to be the destination of his next move. Recall that the Manhattan distance between two points and is defined as .
-
- If two or more points whose Manhattan distance to the airdrop is the same, he will use the following priority rule to break the tie: has the highest priority to be selected, has the second highest priority, has the third highest priority, and has the lowest priority.
-
- At the end of this time unit, he arrives at his destination.
- If the position of a living player at the beginning of this time unit is equal to , he will continue to fatten his backpack with the supplies in the airdrop and stays at .
But the battle is tough and it's almost impossible for all the players to arrive at the airdrop safely. If two or more players meet at point other than , where both and are integers, they will fight and kill each other and none of them survive.
BaoBao is a big fan of the game and is interested in the number of players successfully arriving at the position of the airdrop, but he doesn't know the value of . Given the value of and the initial position of each player, please help BaoBao calculate the minimum and maximum possible number of players successfully arriving at the position of the airdrop for all , where is the set of all integers (note that can be positive, zero or negative).
输入格式
There are multiple test cases. The first line of the input contains an integer , indicating the number of test cases. For each test case:
The first line contains two integers and (, ), indicating the number of players and the value of the airdrop.
For the following lines, the -th line contains two integers and (), indicating the initial position of the -th player.
It's guaranteed that the sum of in all test cases will not exceed , and in each test case no two players share the same initial position.
输出格式
For each test case output one line containing two integers and separated by one space. indicates the minimum possible number of players successfully arriving at the position of the airdrop, while indicates the maximum possible number.
3
3 2
1 2
2 1
3 5
3 3
2 1
2 5
4 3
2 3
1 3
4 3
1 3
0 3
2 2
提示
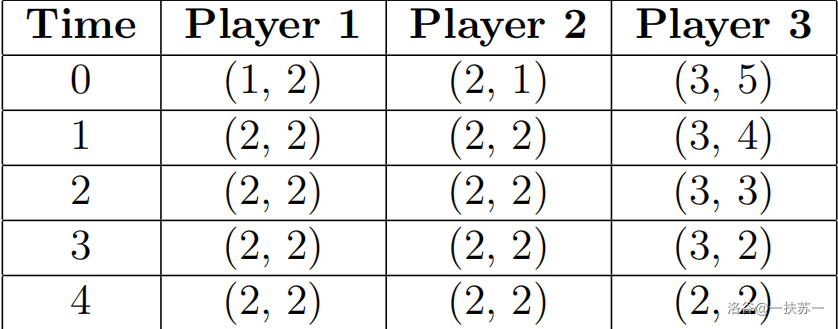
We now explain the first sample test case.
To obtain the answer of , one should consider . The following table shows the position of each player at the end of each time unit when .
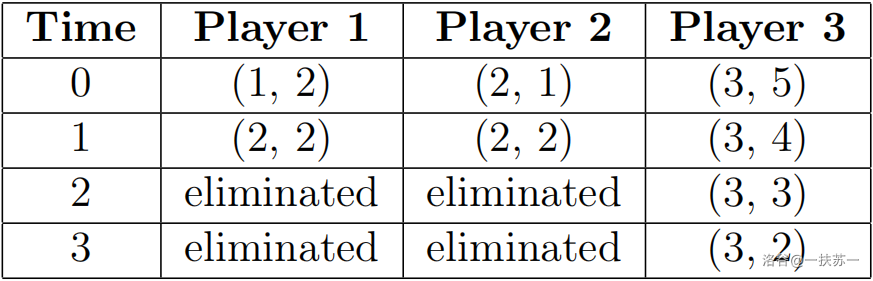
To obtain the answer of , one should consider . The following table shows the position of each player at the end of each time unit when .