题目描述

Paimon has found a tree with $(n + 1)$ initially white vertices in her left pocket and decides to play with it. A tree with $(n + 1)$ nodes is an undirected connected graph with $n$ edges.

Paimon will give you an integer sequence $a_1, a_2, \cdots, a_n$ of length $n$. We first need to select a vertex in the tree and paint it black. Then we perform the following operation $n$ times.

During the $i$-th operation, we select a white vertex $x_i$ which is directly connected with a black vertex $y_i$ by an edge, set the weight of that edge to $a_i$ and also paint $x_i$ in black. After these $n$ operations we get a tree whose edges are all weighted.

What's the maximum length of the diameter of the weighted tree if we select the vertices optimally? The diameter of a weighted tree is the longest simple path in that tree. The length of a simple path is the sum of the weights of all edges in that path.

输入格式

There are multiple test cases. The first line of the input contains an integer $T$ ($1 \le T \le 5 \times 10^3$) indicating the number of test cases. For each test case:

The first line contains an integer $n$ ($1 \le n \le 150$) indicating the length of the sequence.

The second line contains $n$ integers $a_1, a_2, \cdots, a_n$ ($1 \le a_i \le 10^9$) indicating the sequence.

For the following $n$ lines, the $i$-th line contains two integers $u_i$ and $v_i$ ($1 \le u_i, v_i \le n + 1$) indicating that there is an edge connecting vertex $u_i$ and $v_i$ in the tree.

It's guaranteed that there is at most $10$ test cases satisfying $n > 20$.

输出格式

For each test case output one line containing one integer indicating the maximum length of the diameter of the tree.

2
5
1 7 3 5 4
1 3
2 3
3 4
4 5
4 6
1
1000000000
1 2

16
1000000000

提示

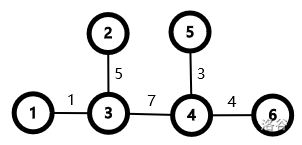
For the first sample test case, we select the vertices in the order of $1, 3, 4, 5, 2, 6$, resulting in the weighted tree of the following image. It's obvious that the longest simple path is of length $16$.