题目描述

Given a convex polygon $P$ with $n$ vertices, you need to choose two vertices of $P$, so that the line connecting the two vertices will split $P$ into two smaller polygons $Q$ and $R$, both with positive area.

Let $d(Q)$ be the diameter of polygon $Q$ and $d(R)$ be the diameter of polygon $R$, calculate the minimum value of $(d(Q))^2 + (d(R))^2$.

Recall that the diameter of a polygon is the maximum distance between two points inside or on the border of the polygon.

输入格式

There are multiple test cases. The first line of the input contains an integer $T$ indicating the number of test cases. For each test case:

The first line contains an integer $n$ ($4 \le n \le 5 \times 10^3$) indicating the number of vertices of the convex polygon $P$.

For the following $n$ lines, the $i$-th line contains two integers $x_i$ and $y_i$ ($0 \le x_i, y_i \le 10^9$) indicating the $i$-th vertex of the convex polygon $P$. Vertices are given in counter-clockwise order. It's guaranteed that the area of the convex polygon is positive, and there are no two vertices with the same coordinate. It's possible that three vertices lie on the same line.

It's guaranteed that the sum of $n$ of all test cases will not exceed $5 \times 10^3$.

输出格式

For each test case output one line containing one integer indicating the answer.

2
4
1 0
2 0
1 1
0 0
6
10 4
9 7
5 7
4 5
6 4
9 3

4
44

提示

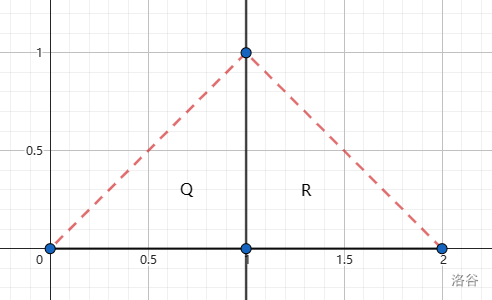
The first sample test case is shown as follows. The diameter of smaller polygons are marked by red dashed segments. In fact, $(1, 0)$ and $(1, 1)$ are the only pair of vertices we can choose in this test case. You can't choose $(0, 0)$ and $(2, 0)$, or $(0, 0)$ and $(1, 1)$, because they can't split $P$ into two smaller polygons both with positive area.

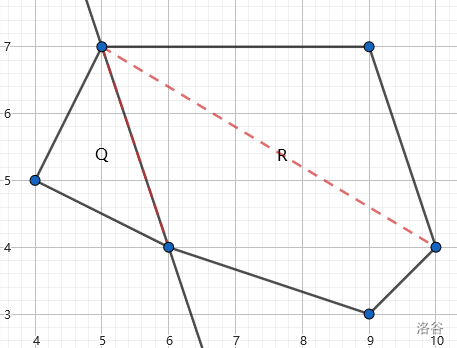
The second sample test case is shown as follows. The diameter of smaller polygons are marked by red dashed segments.