题目背景

What age is it that you are still solving traditional path query problems?

题目描述

After reading the paper Distributed Exact Shortest Paths in Sublinear Time, you have learned how to solve the distributed single-source shortest paths problem in $\mathcal{O}(D^{1/3} \cdot (n \log n)^{2/3})$. To give your knowledge good practice, Little Cyan Fish prepared the following practice task for you.

Little Cyan Fish has a graph consisting of $n$ vertices and $m$ bidirectional edges. The vertices are numbered from $1$ to $n$. The $i$-th edge connects vertex $u_i$ to vertex $v_i$ and is assigned a weight $w_i$.

For any path in the graph between two vertices $u$ and $v$, let's define the value of the path as the bitwise AND of the weights of all the edges in the path.

As a fan of high-value paths, Little Cyan Fish has set a constant threshold $V$. Little Cyan Fish loves a path if and only if its value is at least $V$.

Little Cyan Fish will now ask you $q$ queries, where the $i$-th query can be represented as a pair of integers $(u_i, v_i)$. For each query, your task is to determine if there exists a path from vertex $u_i$ to vertex $v_i$ that Little Cyan Fish would love it.

输入格式

There is only one test case in each test file.

The first line contains four integers $n$, $m$, $q$ and $V$ ($1 \le n \le 10^5$, $0 \le m \le 5 \times 10^5$, $1 \leq q \leq 5 \times 10^5$, $0 \leq V < 2^{60}$) indicating the number of vertices, the number of edges, the number of queries and the constant threshold.

For the following $m$ lines, the $i$-th line contains three integers $u_i$, $v_i$ and $w_i$ ($1 \le u_i,v_i \le n$, $u_i \ne v_i$, $0 \leq w_i < 2^{60}$), indicating a bidirectional edge between vertex $u_i$ and vertex $v_i$ with the weight $w_i$. There might be multiple edges connecting the same pair of vertices.

For the following $q$ lines, the $i$-th line contains two integers $u_i$ and $v_i$ ($1 \leq u_i, v_i \leq n$, $u_i \ne v_i$), indicating a query.

输出格式

For each query output one line. If there exists a path whose value is at least $V$ between vertex $u_i$ and $v_i$ output Yes, otherwise output No.

9 8 4 5
1 2 8
1 3 7
2 4 1
3 4 14
2 5 9
4 5 7
5 6 6
3 7 15
1 6
2 7
7 6
1 8

Yes
No
Yes
No

3 4 1 4
1 2 3
1 2 5
2 3 2
2 3 6
1 3

Yes

提示

We now use $\&$ to represent the bitwise AND operation.

The first sample test case is shown as follows.

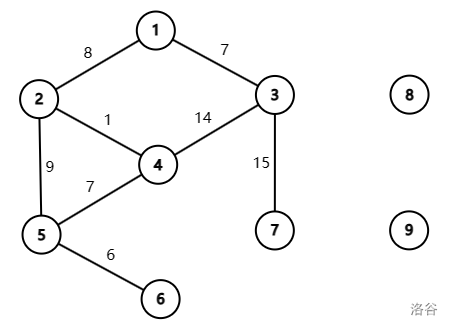
• For the first query, a valid path is $1 \to 3 \to 4 \to 5 \to 6$, whose value is $7 \,\&\, 14 \,\&\, 7 \,\&\, 6 = 6 \ge 5$.
• For the third query, a valid path is $7 \to 3 \to 4 \to 5 \to 6$, whose value is $15 \,\&\, 14 \,\&\, 7 \,\&\, 6 = 6 \ge 5$.
• For the fourth query, as there is no path between vertex $1$ and $8$, the answer is No.

For the only query of the second sample test case, we can consider the path consisting of the $2$-nd and the $4$-th edge. Its value is $5 \,\&\, 6 = 4 \ge 4$.