#P9563. [SDCPC 2023] Be Careful 2
[SDCPC 2023] Be Careful 2
题目背景
警告:滥用本题评测将被封禁。
题目描述
Little Cyan Fish has an rectangle located in a plane. The top-right corner of the rectangle is at , while the bottom-left corner is at . There are banned points inside the rectangle. The -th banned point is located at .
Little Cyan Fish would like to draw a square inside the rectangle. However, he dislikes all the banned points, so there cannot be any banned points inside his square. Formally, Little Cyan Fish can draw a square with the bottom-left corner at and a side length if and only if:
- Both and are non-negative integers while is a positive integer.
- .
- .
- For each , the following condition must NOT be met:
- and .
Please calculate the sum of the areas of all the squares that Little Cyan Fish can possibly draw. Since the answer could be huge, you need to output it modulo .
输入格式
The is only one test case in each test file.
The first line of the input contains three integers , and (, ) indicating the size of the rectangle and the number of banned points.
For the following lines, the -th line contains two integers and (, ) indicating the position of the -th banned point. It is guaranteed that all the banned points are distinct.
输出格式
Output one line containing one integer indicating the answer modulo .
3 3 1
2 2
21
5 5 2
2 1
2 4
126
提示
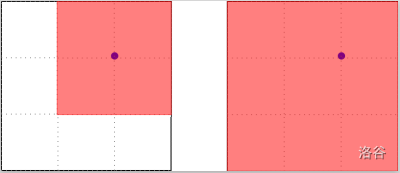
For the first sample test case, Little Cyan Fish has ways to draw a square, illustrated as follows.
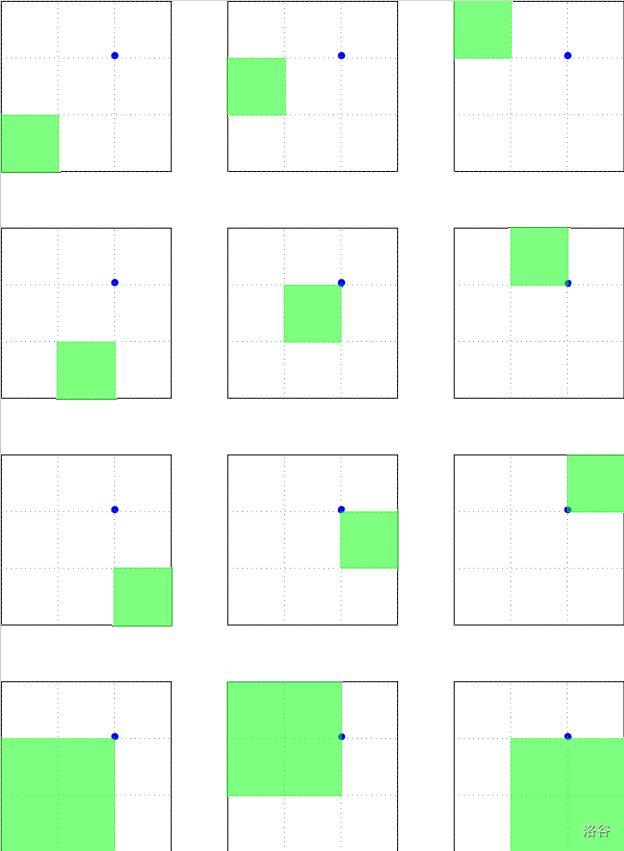
There are squares of side length and squares of side length . So the answer is .
Note that the following plans are invalid since there's a banned point in the square.