第一次写 s 组题解 qwq

废话

如果我说。。。

这个是 找规律的模拟题。

你会震惊嘛（）

怎么想到思路的

假如 $n = 3$ ，可以打个表。

k	ans
0	0 0 0
1	0 0 1
2	0 1 1
3	0 1 0
4	1 1 0
5	1 1 1
6	1 0 1
7	1 0 0

仔细发现，1分布的位置成块状分布，如第一位的0全在 $0 \sim 3$ 之间，1全在 $4 \sim 7$ 之间，而 $k = 3$ 时正好是一半的位置！！！

这难道就是规律？！

读读题昂。。

n 位格雷码不止一种，下面给出其中一种格雷码的生成算法：

1. 1 位格雷码由两个 1 位二进制串组成，顺序为：0，1。
2. n + 1n+1 位格雷码的前 2^n2n 个二进制串，可以由依此算法生成的 nn 位格雷码（总共 2^n2n 个 nn 位二进制串）按顺序排列，再在每个串前加一个前缀 0 构成。
3. n + 1n+1 位格雷码的后 2^n2n 个二进制串，可以由依此算法生成的 nn 位格雷码（总共 2^n2n 个 nn 位二进制串）按逆序排列，再在每个串前加一个前缀 1 构成。

请注意第三点中的“逆序”，否则你20分（。。比没开 long long 的还要惨。。）

所以。。思路是

一共有 $n$ 位，所以 $n$ 次循环。

从 $n$ 循环到 $1$ ，第 $i$ 次时判断 $k$ 在中间数的前边还是后边。若是前边那就输出0，否则输出1，记得做逆序处理。

满分了？

#include <iostream>
#include <cmath>
#include <string>

int n, k; // 1 input
std:: string ans; // 2 output
long long tmp;

int main () {
	std:: cin >> n >> k; // 1 input
	for (int i = n; i >= 1; i--) {
		long long tmp = std:: pow (2, i - 1) - 1; // 3 middle number
		if (k <= tmp) {
			ans = ans + "0";
		} // if
		else {
			ans = ans + "1";
			k = std:: pow (2, i) - 1 - k; // 4 res' order
		} // else
	} // for
	std:: cout << ans << "\n";
	return 0;
}

85分。。好吧

看看范围哈 $1 \leq n \leq 64$ , $0 \leq k \lt 2^n$

你会发现 $k$ 的范围到了 $2^n$ 啊啊啊啊啊啊

long long 显然还不够大诶。。

unsigned long long，启动！

全对了！吗？

#include <iostream>
#include <cmath>
#include <string>

unsigned long long n, k; // 1 input
std:: string ans; // 2 output
unsigned long long tmp; // 3 middle number

int main () {
	std:: cin >> n >> k; // 1
	for (int i = n; i >= 1; i--) {
		tmp = std:: pow (2, i - 1) - 1; // 3
		if (k <= tmp) {
			ans = ans + "0";
		} // if
		else {
			ans = ans + "1";
			k = std:: pow (2, i) - 1 - k; // 4 res' order
		} // else
	} // for
	std:: cout << ans << "\n";
	return 0;
}

这不是开了unsigned long long 嘛！！！！！！

其实是 cmath 的 pow() 爆掉了啊啊啊啊啊啊

pow() 似乎达不到 unsigned long long 那么大哦。。。

打表叭

尊的 $AC$ 了

#include <iostream>
#include <string>

unsigned long long n, k; // 1 input
std:: string ans; // 2 output
unsigned long long tmp; // 3 middle number

unsigned long long pow[70]= {1,2,4,8,16,32,64,
           128,256,512,1024,2048,4096,
           8192,16384,32768,65536,131072,262144,
           524288,1048576,2097152,4194304,8388608,16777216,
           33554432,67108864,134217728,268435456,536870912,1073741824,
           2147483648,4294967296,8589934592,17179869184,34359738368,68719476736,
           137438953472,274877906944,549755813888,1099511627776,2199023255552,4398046511104,
           8796093022208,17592186044416,35184372088832,70368744177664,140737488355328,281474976710656,
           562949953421312,1125899906842624,2251799813685248,4503599627370496,9007199254740992,18014398509481984,
           36028797018963968,72057594037927936,144115188075855872,288230376151711744,576460752303423488,1152921504606846976,
           2305843009213693952,4611686018427387904,9223372036854775808
          }; // 4 pow

int main () {
	std:: cin >> n >> k; // 1
	for (int i = n; i >= 1; i--) {
		tmp = pow[i - 1] - 1; // 3
		if (k <= tmp) {
			ans = ans + "0";
		} // if
		else {
			ans = ans + "1";
			k = pow[i] - 1 - k; // 5 res' order
		} // else
	} // for
	std:: cout << ans << "\n";
	return 0;
}

虽然unsigned long long只能存到 $2^{64} - 1$，但可以通过反溢出的“逆天操作”用bug解决bug。

所以。。

满昏！！！！！！！！！！

题解(bitset版）

更好的阅读体验点这里

part.1 什么是格雷码

格雷码（Gray Code）是一种特殊的二进制编码方式，其核心特性在于：任意两个相邻的数之间仅有一位二进制位不同。这种特性使得格雷码在许多工程和算法问题中具有广泛应用，例如减少数字转换过程中的出错概率、优化状态转移等。

part.2 二进制转格雷码

我们可以用一种“列竖式”的方式将二进制转化为格雷码

需要的知识点-异或&二进制

我们以3（二进制为0011为例）

首先，列一个竖式

方法：

步骤一：将相同的数字下移然后向右移$1$位，进行异或运算

如图所示

附件-异或：

异或是在各种计算机语言中，如C、C++、java等，使用按位异或的思想执行的操作。异或逻辑的关系是：当AB不同时，输出$P=1$；当AB相同时，输出$P=0$。“⊕”是异或数学运算符号

步骤二：进行按位异或运算

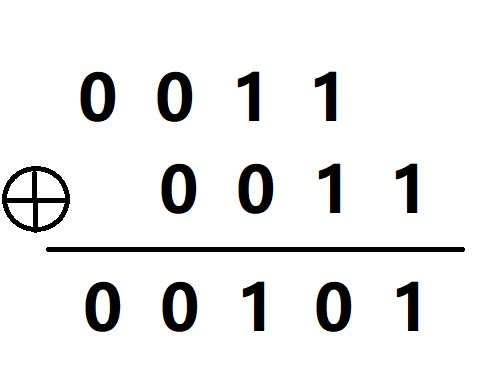
解释：

1.第一位只有一个$0$，抄下来 2.第二位两个$0$，相同，故为零 3.第三位一个$1$一个$0$,不同，故为一 4.第四位两个$1$，相同，故为零 5.第五位只有一个$1$，抄下来 6.故答案为$00101$

步骤三：去掉最后一位

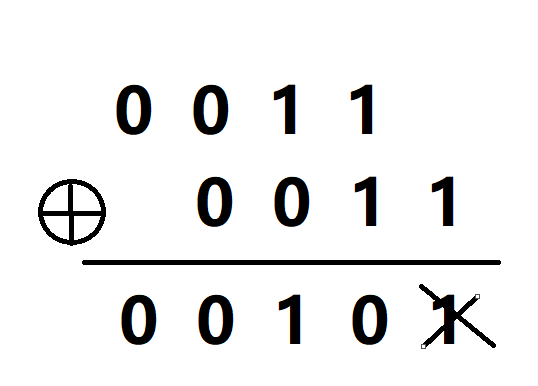
故3的格雷码为0010

---

part.3 题目解读

题目原文

P5657 [CSP-S2019] 格雷码

题目描述

通常，人们习惯将所有 $n$ 位二进制串按照字典序排列，例如所有 2 位二进制串按字典序从小到大排列为：00，01，10，11。

格雷码（Gray Code）是一种特殊的 $n$ 位二进制串排列法，它要求相邻的两个二进制串间恰好有一位不同，特别地，第一个串与最后一个串也算作相邻。

所有 2 位二进制串按格雷码排列的一个例子为：00，01，11，10。

$n$ 位格雷码不止一种，下面给出其中一种格雷码的生成算法：

1. 1 位格雷码由两个 1 位二进制串组成，顺序为：0，1。
2. $n + 1$ 位格雷码的前 $2^n$ 个二进制串，可以由依此算法生成的 $n$ 位格雷码（总共 $2^n$ 个 $n$ 位二进制串）按顺序排列，再在每个串前加一个前缀 0 构成。
3. $n + 1$ 位格雷码的后 $2^n$ 个二进制串，可以由依此算法生成的 $n$ 位格雷码（总共 $2^n$ 个 $n$ 位二进制串）按逆序排列，再在每个串前加一个前缀 1 构成。

综上，$n + 1$ 位格雷码，由 $n$ 位格雷码的 $2^n$ 个二进制串按顺序排列再加前缀 0，和按逆序排列再加前缀 1 构成，共 $2^{n+1}$ 个二进制串。另外，对于 $n$ 位格雷码中的 $2^n$ 个 二进制串，我们按上述算法得到的排列顺序将它们从 $0 \sim 2^n - 1$ 编号。

按该算法，2 位格雷码可以这样推出：

1. 已知 1 位格雷码为 0，1。
2. 前两个格雷码为 00，01。后两个格雷码为 11，10。合并得到 00，01，11，10，编号依次为 0 ~ 3。

同理，3 位格雷码可以这样推出：

1. 已知 2 位格雷码为：00，01，11，10。
2. 前四个格雷码为：000，001，011，010。后四个格雷码为：110，111，101，100。合并得到：000，001，011，010，110，111，101，100，编号依次为 0 ~ 7。

现在给出 $n$，$k$，请你求出按上述算法生成的 $n$ 位格雷码中的 $k$ 号二进制串。

输入格式

仅一行两个整数 $n$，$k$，意义见题目描述。

输出格式

仅一行一个 $n$ 位二进制串表示答案。

。

【数据范围】

对于 $50\%$ 的数据：$n \leq 10$

对于 $80\%$ 的数据：$k \leq 5 \times 10^6$

对于 $95\%$ 的数据：$k \leq 2^{63} - 1$

对于 $100\%$ 的数据：$1 \leq n \leq 64$, $0 \leq k \lt 2^n$

---

简化：n代表格雷码的位数，k代表格雷码的十进制，就是把k化成n位的格雷码

---

part.4 题目思路

1.将k转化为二进制

可以使用bitset 不会bitset点此了解

string b=bitset<64>(k).to_string();

意思：将k转化为64位的二进制，并且用s存起来

2.将s转化为n位

因为bitset中的位数只支持常数，所以我们只能声明初始为数据范围的最大值（64位）

所以我们要保留s的后n位，可以使用函数substr

b=b.substr(64 - n);

3.将二进制转化为格雷码

参考上文，递推式为

$$if_{b_i=b_i-1},gray_i=0$$ $$if_{b_i\not=b_i-1},gray_i=1$$

代码

#include<bits/stdc++.h>
using namespace std;
int main() {
   unsigned long long n,k;
   cin>>n>>k;
   string b=bitset<64>(k).to_string(),gray;
   b=b.substr(64 - n);
   gray+=b[0]; 
   for(int i=1;i<n;i++) gray+=(b[i]==b[i-1])?'0':'1';
   cout<<gray;
   return 0;
}