题目描述

A fishing village built on the surface of a frozen lake far north in the arctic is endangered by global warming-fractures are starting to form on the lake surface. The village consists of n igloos of spherical shape, each occupying a circular area of the surface.

An igloo can be represented as a circle in the coordinate plane: the center of the circle is a point with integer coordinates, while the radius is a positive floating-point number less than 1 with exactly one fractional digit.

Given the locations of possible ice fractures, the villagers would like to know how many igloos are affected by each. Formally, given q queries where each query is a straight line segment defined by the two endpoints, find the number of igloos each segment intersects. A segment intersects an igloo if it has at least one point in common with the interior of the circle.

输入格式

The first line contains an integer n (1≤n≤100000) - the number of igloos. Each of the following n lines contains three numbers x, y and r – the coordinates of the center and the radius of one igloo. The coordinates x and y are integers such that 1≤ x, y≤500, while r is a floating-point number with exactly one fractional digit such that 0 < r < 1. No two igloos will intersect or touch.

The following line contains an integer q (1 ≤ q ≤ 100000) - the number of queries. Each of the following q linescontainsfourintegers x1, y1, x2, y2 (1≤ x1, y1, x2, y2 ≤500)-thecoordinatesofthe two endpoints of the segment. The two endpoints will be different. Endpoints may be inside igloos.

You may assume that, for every igloo i and the segment s, the square of the distance between s and the center of i is either less than r2−10−5 or greater than r2 +10−5 where r is the radius of the igloo i.

输出格式

Output should consist of q lines. The k-th line should contain a single integer – the number of igloos that are intersected by the k-th segment.

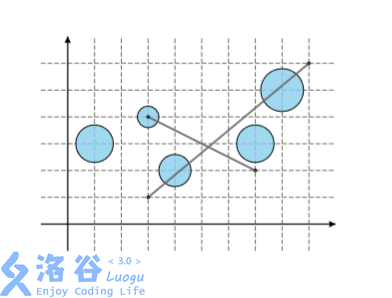
5 
4 2 0.6 
7 3 0.7 
8 5 0.8 
1 3 0.7 
3 4 0.4 
2 
3 1 9 6 
3 4 7 2

2
1

提示

Central Europe Regional Contest 2015 Problem I