题目描述
现在共有 n 个存在于平面直角坐标系中的村庄,国家颁布了乡村振兴的政策,你负责修建一个 6G 信号基站让村民们都过上有网用的好日子。山地地形险要,在不同的地区修建基站的成本将会提升。
我们定义信号基站坐标为 (a,b),信号强度为 R,则一个位于 (x,y) 的村庄能够接受到信号当且仅当 R2≥(x−a)2+(y−b)2。在 (a,b) 修建一个信号强度为 R 的信号基站的成本为 R×w(a,b)。其中 w(a,b) 为该地区的修建难度。
经过地形勘测,你已经得知了地区的修建难度的具体数值,具体地。w(a,b) 由一个圆形区域来决定,该圆有以下属性:圆心 (x,y),半径 r,权值 v。若 (a,b) 在圆内(包含圆周上)则 w(a,b)=v,若 (a,b) 被多个圆包含则取 v 的最大值,若 (a,b) 未被任何圆包含,则 w(a,b)=1。这些圆形区域共有 m 个。
你需要修建一个基站使得所有村庄都能接受到信号且修建的成本最小。
输入格式
第一行两个整数 n,m。
随后 n 行,每行两个整数 x,y,表示村庄坐标。
随后 m 行,每行先是三个整数 x,y,r,然后是一个至多 2 位小数的实数 v,表示一个特殊区域。
输出格式
输出最小成本,你需要保证答案与标准答案的绝对误差或相对误差不超过 10−5。即设你的答案为 a,标准答案为 A,你需要保证 min(∣a−A∣,A∣a−A∣)≤10−5。
3 0
1 2
2 1
2 3
1.0000000000
2 0
1 1
2 2
0.7071067811
2 1
2 0
0 2
0 0 2 5.00
1.5307337295
提示
【样例 1 解释】
如下图
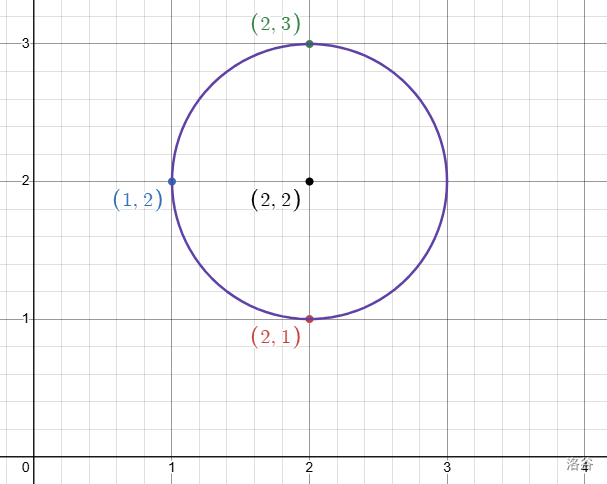
【样例 2 解释】
你可以将基站建设于非整数点上。答案为 22,你也可以输出 0.707106781 等。
【数据范围与约定】
对于所有的数据,保证:
- 1≤n≤104,
- 0≤m≤8,
- 0≤x,y,r≤105,
- 0<v≤10。
- 点坐标可能重复。
::cute-table{tuack}
| Subtask |
n≤ |
m |
x,y |
分值 |
| 1 |
10 |
≤3 |
≤5 |
20 |
| 2 |
104 |
=0 |
≤105 |
30 |
| 3 |
≤8 |
50 |
保证数据随机生成。
生成方式:给定 $\mathrm{maxx},\mathrm{maxy},\mathrm{maxr},\mathrm{maxv}$,则每个 (x,y) 在 [0,maxx],[0,maxy] 的范围内随机均匀生成;每个 r 在 [0,maxr] 的范围内随机均匀生成;每个 v 在 [0,maxv] 的范围内随机均匀生成且为实数。

