题目背景

试题来源：https://koi.or.kr/archives/。中文翻译做了少量本土化修改。

按照署名—非商业性使用—相同方式共享 4.0 协议国际版进行授权。

题目描述

我们可以考虑 1 维空间中的线段、2 维空间中的矩形、3 维空间中的长方体：

• 线段的大小可以用变量 $A$ 表示，其长度为 $A$；
• 矩形的大小可以用两个变量 $A$ 和 $B$ 表示，其面积为 $A \cdot B$；
• 长方体的大小可以用三个变量 $A$、$B$、$C$ 表示，其体积为 $A \cdot B \cdot C$。

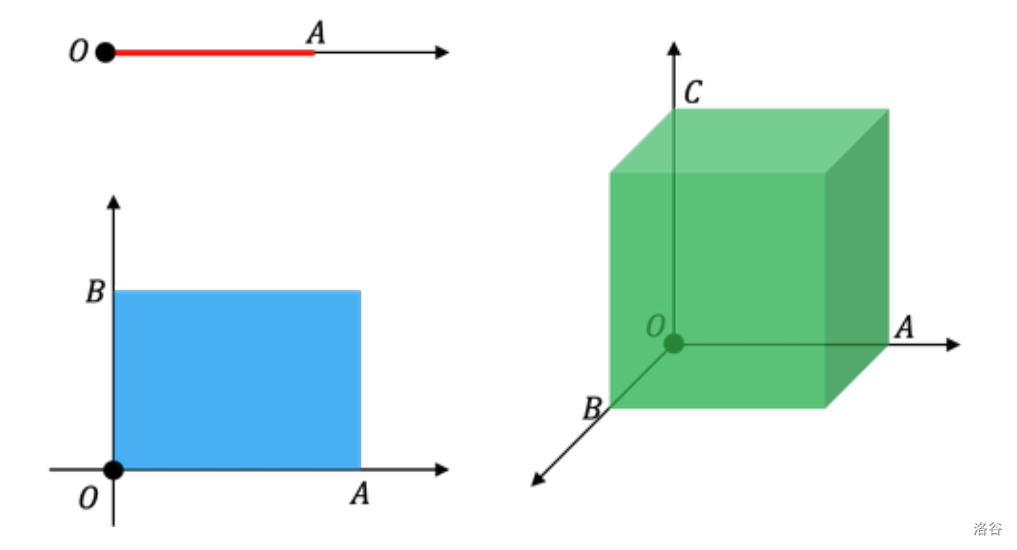
在四维空间中，可以定义一个由四个变量 $A$、$B$、$C$、$D$ 表示大小的“超矩形”。其“体积”为 $A \cdot B \cdot C \cdot D$。

起初，变量 $A$、$B$、$C$、$D$ 的值分别为 $A_0$、$B_0$、$C_0$、$D_0$。

你有 $N$ 张“卡牌”，每张卡牌上写有一个字母 $T_i$（在 $A$、$B$、$C$、$D$ 中取一个）和一个正整数 $U_i$，表示该卡牌会使对应变量的值增加 $U_i$。每张卡牌最多只能使用一次，用完即消失。

你希望通过恰好选用 $K$ 张卡牌（选出的卡牌可以按任意顺序使用），来最大化超矩形的体积。请编写程序，输出一组选牌及使用顺序，使体积最大化。

若存在多种方式达到最大体积，任选其中一种方案输出即可。

输入格式

第一行输入两个整数 $N$ 和 $K$，中间以空格隔开。
第二行输入初始变量值 $A_0$、$B_0$、$C_0$、$D_0$，中间以空格隔开。
接下来的 $N$ 行中，第 $i$ 行输入第 $i$ 张卡牌的内容，即 $T_i$ 和 $U_i$，中间以空格隔开。

输出格式

输出 $K$ 行，依次表示选中的卡牌及其使用顺序，按与输入格式相同的方式给出。

4 3
1 1 1 1
A 1
A 1
A 2
A 2

A 2
A 1
A 2

8 6
1 2 3 4
A 2
A 5
B 7
B 2
C 5
C 9
D 1
D 3

A 2
B 7
C 5
A 5
C 9
D 3

提示

约束条件

• 所有给定数值均为整数
• $1 \leq K \leq N \leq 200\,000$
• $1 \leq A_0, B_0, C_0, D_0 \leq 1\,000\,000$
• 对所有 $1 \leq i \leq N$，$T_i \in \{A, B, C, D\}$
• 对所有 $1 \leq i \leq N$，$1 \leq U_i \leq 1\,000\,000$

子任务

1. （8 分）$N \leq 10$，$A_0, B_0, C_0, D_0 \leq 10$，且所有 $U_i \leq 10$
2. （6 分）$B_0 = C_0 = D_0 = 1$，所有 $T_i = A$
3. （15 分）$N \leq 300$，$A_0, B_0, C_0, D_0 \leq 100$，所有 $U_i \leq 100$
4. （21 分）所有 $U_i = 1$
5. （20 分）$D_0 = 1$，所有 $T_i \in \{A, B, C\}$，所有 $U_i \leq 10$
6. （30 分）无附加约束条件