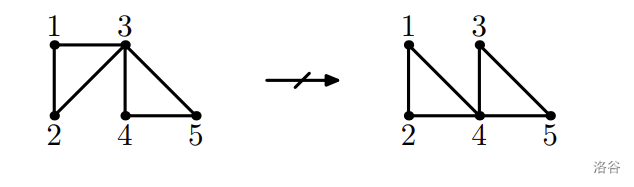题目描述

In the university, Caroline started to learn about cactus graphs. Her teacher wanted to check whether the students really understood the definition of a cactus or not and gave them the following problem as a home assignment:

You are given two cactuses with the same number of vertices and edges. Your task is to answer whether it is possible to transform the first cactus into the second one using only the following two-step operation at most $15\,000$ times:

• Pick an arbitrary edge from the first cactus and remove it (note that after this action, it's not necessary that graph is a cactus);
• Add an arbitrary non-existing edge into the first graph, so that the graph becomes a cactus.

Note that the operation consists of both actions, so you must apply both actions.

It's guaranteed that if it's possible to transform the first cactus into the second one, then it can be done by using at most $15\,000$ operations.

The teacher promised to give a perfect grade without an exam to anyone who solved the problem. Since the given cactuses are big and Caroline can't solve the problem independently in this short period of time, she asked you to help her write a program that solves the problem.

A cactus is a connected undirected graph in which every edge lies on at most one simple cycle. Intuitively, a cactus is a generalization of a tree where some cycles are allowed. Multiedges (multiple edges between a pair of vertices) and loops (edges that connect a vertex to itself) are not allowed in a cactus.

Two cactuses are called same if for any pair of vertices $v$ and $u$ ($1 \leq v < u \leq n$), either there exists an edge $(v, u)$ in both cactuses or does not.

输入格式

The first line contains two integers $n$ and $m$ ($3 \le n \le 1000$, $n - 1 \le m \le \lfloor \frac{3(n - 1)}{2} \rfloor$) --- the number of vertices and edges in the cactuses. Each of the next $2 \cdot m$ lines contains two integers $u$ and $v$ ($1 \le u \ne v \le n$) --- the edges of the cactuses. The first $m$ lines represent the first cactus, while the second $m$ lines represent the second cactus.

输出格式

If transforming the first cactus into the second one is impossible, output the single line with the word NO.

Otherwise, in the first line output the single word YES. In the second line output an integer $c$ ($0 \leq c \leq 15\,000$) --- the number of operations. Each of the following $c$ lines should contain four integers $w_i$ ($1 \le i \le 4$, $1 \le w_i \le n$). The first two integers ($w_1$, $w_2$) represent the vertices of the removed edge, while the last two integers ($w_3$, $w_4$) represent the vertices of the added edge.

5 5
1 2
3 1
2 4
3 4
4 5
1 2
3 2
3 1
4 1
3 5

YES
3
3 4 2 3
5 4 3 5
2 4 1 4

5 6
1 2
2 3
1 3
4 3
3 5
5 4
1 2
2 4
4 1
4 3
3 5
4 5

NO

提示

Sample 1 Explanation

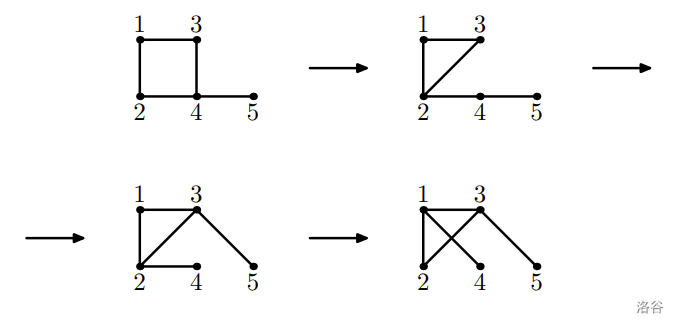
Sample 2 Explanation