题目描述

You play a game with multiple fair six-sided dice. Each die's face displays a single symbol. The objective of the game is to roll the dice and create a valid word from the symbols on top of each die. If you cannot form a word, you may reroll the dice for another attempt.

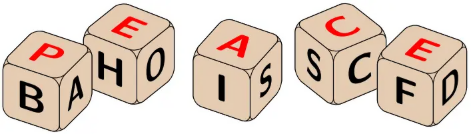
Figure K.1: Five dice making a valid word corresponding to Sample Input 1.

Suppose there are five dice: one of them contains letters A, B, C, D, E, and P (abbreviated as ABCDEP), and the other dice contain letters AEHOXU, AISOLR, ABCDEF, and ABCSCC. The first roll yields the following letters on the tops of respective dice: P, X, R, E, and S. As it is impossible to arrange these letters into a valid word, you decide to keep the P, S, and E, and reroll the other dice, in an attempt to make words like PARSE, PAUSE, PHASE, POISE, PROSE, PULSE, or PURSE. The two dice yield E and A, resulting in the following five letters: P, E, A, E, and S. You still cannot think of a valid word, so you decide to keep four letters and reroll only the last die, which has three sides with letter C. By doing so, there is a $50\%$ chance that it will be possible to make a final valid word: PEACE, as shown in Figure K.1.

When you roll a die, it lands on any one of its faces with equal probability. What is the expected number of rolls needed to make a valid word, assuming you use an optimal strategy?

输入格式

The first line of input contains two numbers $d$ and $w$, where $d$ ($1 \le d \le 6$) is the number of dice and $w$ ($1 \le w \le 2\cdot 10^5$) is the number of valid words in the dictionary. The following $d$ lines each have $6$ symbols, one for each face of the die. The final $w$ lines contain $w$ distinct valid words in the dictionary. Every word has exactly $d$ symbols.

All symbols in the input are either uppercase letters (A-Z) or digits (0-9).

输出格式

If it is possible to make a valid word, output the expected number of rolls needed to make a valid word when using an optimal strategy. Otherwise, output impossible. Your answer should have an absolute or relative error of at most $10^{-6}$.

5 8
ABCDEP
AEHOXU
AISOLR
ABCDEF
ABCSCC
PARSE
PAUSE
PHASE
POISE
PROSE
PULSE
PURSE
PEACE

9.677887141

2 1
AAAAAA
BBBBBB
AB

1.0

3 1
123456
123456
123456
666

10.555444555

2 1
ABCDEF
GHI234
AB

impossible