题目描述

Two players are playing a game on a tape divided into cells that is infinite to the right. The cells are numbered with $1, 2, 3, \ldots$ from left to right. Each cell $x$ is adjacent to cells $x - 1$ and $x + 1$, except for cell $1$, which is only adjacent to cell $2$.

There is a finite number of red chips (the first player's chips) and blue chips (the second player's chips) on the tape. Each cell contains either several red chips, or several blue chips, or no chips at all.

The players take turns. On their turn, a player can either skip the turn or take one of their chips and move it to an adjacent cell. If there are no opponent's chips in the adjacent cell, the turn ends; if there is at least one opponent's chip there, one chip from each player is removed from that cell --- thus, at the end of the turn, there will still be no two chips of different colors in the same cell.

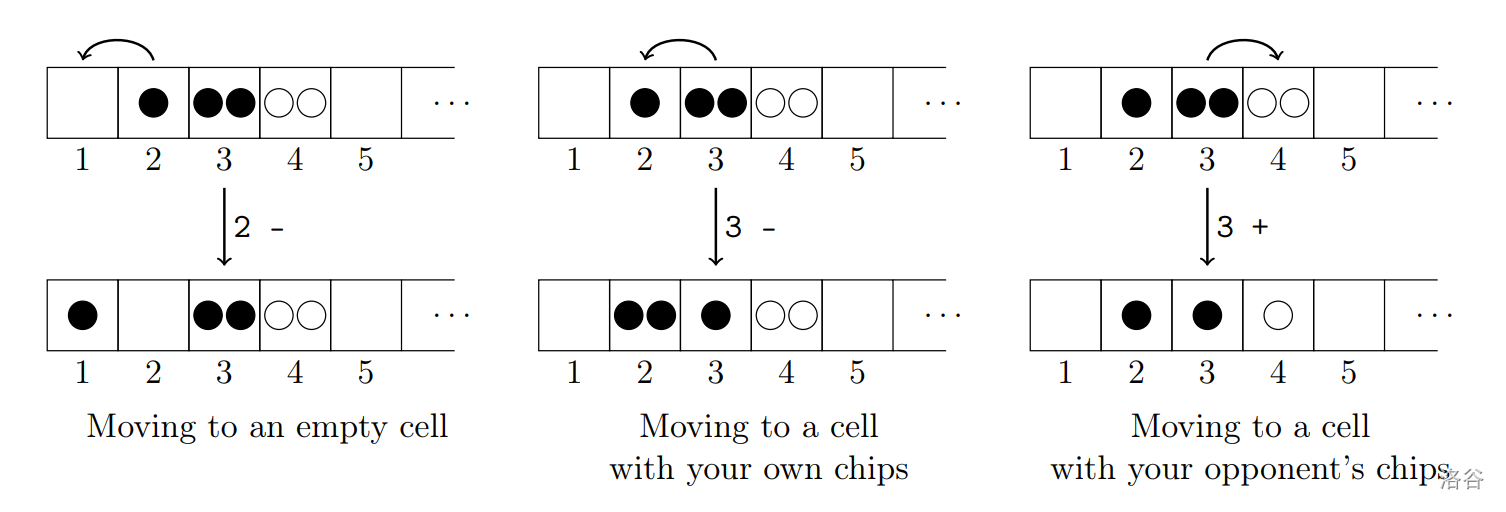
If both players run out of chips, the game ends in a draw. If only one player runs out of chips, they are declared the loser, and their opponent is declared the winner. Finally, if after $10^{100}$ turns the game has not ended, it is forcibly concluded and declared a draw.

You are given the initial setup of the tape. Determine who will win with perfect play from both players, and find any optimal first move for the first player.

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1 \le t \le 10^4$). The description of the test cases follows.

The first line of each test case contains a single integer $n$, denoting the number of cells that initially contain at least one chip ($2 \le n \le 2 \cdot 10^5$).

The $i$-th of the following $n$ lines contains two integers $x_i$, $m_i$, and a character $c_i$, denoting the coordinate of the $i$-th non-empty cell from the left, the number of chips in it, and the color of these chips ($1 \le x_1 < x_2 < \cdots < x_n \le 10^6$; $1 \le m_i \le 10^6$; $c_i \in \{\mathtt{R}, \mathtt{B}\}$). There is at least one chip of each color on the tape.

It is guaranteed that the sum of $n$ over all test cases does not exceed $2 \cdot 10^5$.

输出格式

For each test case, print:

• $\texttt{First}$ $x$ $d$, if the first player (moving red chips) will win;
• $\texttt{Second}$, if the second player (moving blue chips) will win;
• $\texttt{Draw}$ $x$ $d$, if the outcome of the game will be a draw.

In the first and third cases, $x$ $d$ specifies any winning or drawing move, respectively --- that is, a move after which, with perfect play from the second player, there remains a possibility to win or draw the game. Here, $x$ is the coordinate of the red chip that the first player should move, and $d \in \{\texttt{-}, \texttt{+}\}$ is the direction of the move ($\texttt{-}$ means the chip should be moved to cell $x - 1$, and $\texttt{+}$ means the chip should be moved to cell $x + 1$). If $d$ is $\texttt{-}$, then $x$ must be greater than $1$. If you suggest that the first player skips their turn, print $\texttt{0 0}$ instead of $x$ $d$.

You can print each letter in upper- or lowercase: for instance, the strings $\texttt{First}$, $\texttt{FIRST}$, $\texttt{fiRST}$ will be considered equivalent by the checker.

10
2
1 1 R
2 1 B
2
1 1 B
2 1 R
2
1 2 B
4 1 R
4
1 1 B
2 1 R
4 3 B
6 1 R
2
1 2 B
3 1 R
2
1 2 B
2 1 R
2
1 1 R
2 2 B
2
1 2 R
3 1 B
3
1 1 R
2 1 R
4 1 B
2
1 2 R
2 1 B

Draw 0 0
Draw 2 -
Draw 4 -
Draw 2 -
Draw 0 0
Draw 2 +
Second
Draw 0 0
Draw 2 -
First 1 +

提示

In the last test case, there is only one possible move besides $\texttt{1 +}$, namely, $\texttt{0 0}$ (skip the turn). It is a drawing move, though; hence, it will not be accepted.