题目描述

In Isengard, wizard Saruman, with the help of some magic spells, organized a transport system between $n$ towers. To be precise, he created $m$ one-directional passages, each connecting two towers. Each passage $i$ has some number $t_i$ associated with it, meaning the time it takes, in seconds, for an orc to travel along it. In other words, Saruman's transport system can be represented with a directed weighted graph.

On December 15th, Saruman, sitting in the middle tower called $\textit{Orthanc}$, gets a message from Sauron (via palantir) which says that a valuable present is already near Isengard's entrance tower. So, Saruman needs to instruct the garrison to select one of the orcs and send them with a gift along the shortest path from the entrance tower to Orthanc.

Unfortunately, orcs... aren't exactly smart fellas. Although they are able to drag a load along passages in the transport system and they (at least, in principle) know where Orthanc is, orcs have a really poor understanding of the concept of the shortest path. To make everyone's lives easier, on some towers Saruman puts a huge flashing pointer which says $\textbf{TO ORTHANC~--- THIS WAY}$ and points to one of the passages leading from this tower. Saruman wants orcs to reach Orthanc as fast as possible --- hence, a flashing pointer can only point to a passage that lies on one of the shortest paths to Orthanc. Formally, the flashing pointer on the tower $u$ can point to a passage $\vec{a} = \overrightarrow{uv}$ only if $\mathop{\overrightarrow{\mathrm{dist}}}(v, O) < +\infty$ and $\mathop{\overrightarrow{\mathrm{dist}}}(u, O) = t_{\vec{a}} + \mathop{\overrightarrow{\mathrm{dist}}}(v, O)$. Here by $\mathop{\overrightarrow{\mathrm{dist}}}(x, y)$ we denote the minimum time it takes to get to tower $y$ from tower $x$ (or $+\infty$ if there is no oriented path from $x$ to $y$), by $O$ we denote the tower of Orthanc, and by $u$ and $v$ we denote the starting and the finishing towers of the passage $\vec a$. Note that Saruman will not put a flashing pointer onto Orthanc, nor will he put it on any tower from which Orthanc is unreachable. On each of the remaining towers, he will put exactly one flashing pointer.

This still does not work perfectly well. While traveling to Orthanc, each time an orc is near some tower (any but Orthanc), the orc can either choose a marked passage with Saruman's sign or do some $\textit{hanging around}$, as Saruman calls it, when the orc chooses an outgoing passage completely at random. For any orc, there exists an integer $d$ such that when they're given an order to go to Orthanc, during the commute the orc never chooses to hang around more than $d$ times. This exact number we will politely call this orc's $\textit{incompetence}$.

Note that at some moment it may happen that an orc finds themselves near a tower from which there is no oriented path to Orthanc. Under these unfortunate circumstances, even the least competent orc will find no flashing pointer on the tower, figure out that their mission has failed, stop immediately, and wait for a rescue operation.

Saruman knows that his servants are not very brilliant minds, so he does not expect the delivery of the present to be quick, but he wants it to be successful at the very least. Therefore, it makes sense to assign to this task as competent an orc as possible; on the other hand, competent orcs are rare and pulling them out of their current activities may entirely disrupt those activities. Hence, given the description of Isengard's transport system, find the maximum number $d$ such that there exists a way Saruman can put the flashing pointers, so that an orc with a level of incompetence equal to $d$ can be assigned to deliver the present from the entrance tower and is guaranteed to carry out the order with success, reaching Orthanc.

输入格式

The first line contains two integers $n$ and $m$ --- the number of towers and the number of one-directional passages between them ($2 \le n \le 4 \cdot 10^5$; $0 \le m \le 4 \cdot 10^5$). In the next $m$ lines the descriptions of the passages follow. Each line contains three integers $u_i$, $v_i$, $t_i$ --- the numbers of the starting and the ending towers of a passage, and the number of seconds it takes for a loaded orc to travel along this passage ($1 \le u_i, v_i \le n$; $1 \le t_i \le 10^6$). There can be several passages between the same pair of towers, in any direction, as well as passages that lead from a tower to itself --- in other words, loops, multiple passages, and symmetric pairs of passages are allowed.

The entrance tower is numbered $1$ and Orthanc is numbered $n$.

输出格式

Print one integer $d$ --- the maximum incompetence of an orc who is guaranteed to complete the delivery. If with any level of incompetence it is possible, print the number $n$ (the number of towers). On the other hand, if with any level of incompetence it is impossible, print $-1$.

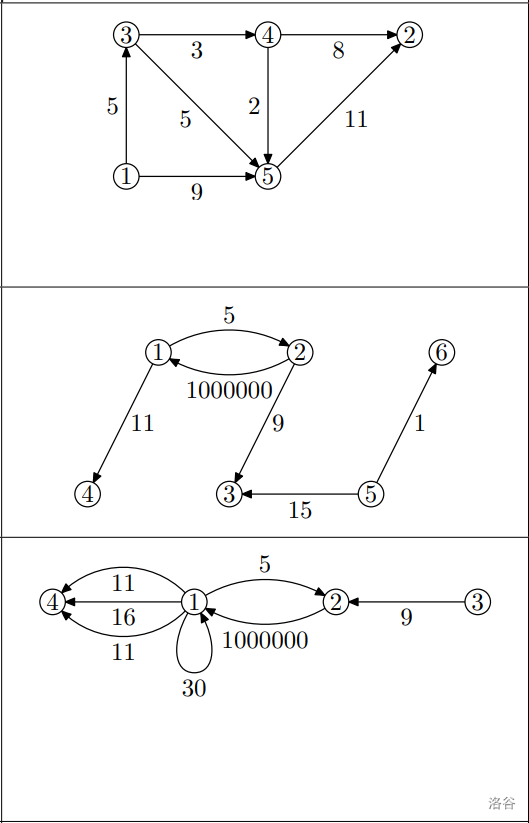
5 7
1 3 5
4 5 2
3 4 3
1 5 9
4 2 8
5 2 11
3 5 5

2

6 6
1 2 5
2 3 9
1 4 11
2 1 1000000
5 3 15
5 6 1

-1

4 7
1 2 5
1 1 30
3 2 9
1 4 11
1 4 16
2 1 1000000
1 4 11

4

2 0

-1

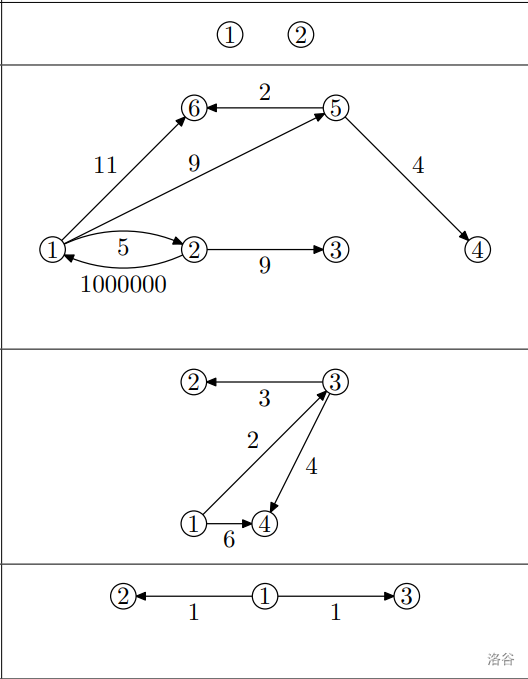
6 7
1 2 5
2 3 9
1 6 11
2 1 1000000
1 5 9
5 6 2
5 4 4

1

4 4
1 4 6
1 3 2
3 2 3
3 4 4

1

3 2
1 2 1
1 3 1

0

提示

All samples' illustrations are shown below: