题目描述

小 $\mathbf A$ 和小 $\mathbf B$ 正在玩一个有趣的游戏。

游戏将在一个 $\underbrace{2\times2\times2\times\cdots\times2}_{k 个 2}$ 的 $k$ 维空间中进行。最小的节点的坐标为 $(\underbrace{0,0,0,\cdots,0}_{k个0})$，最大的节点的坐标为 $(\underbrace{1,1,1,\cdots,1}_{k个1})$。

下面是 $k=3$ 时的情况：

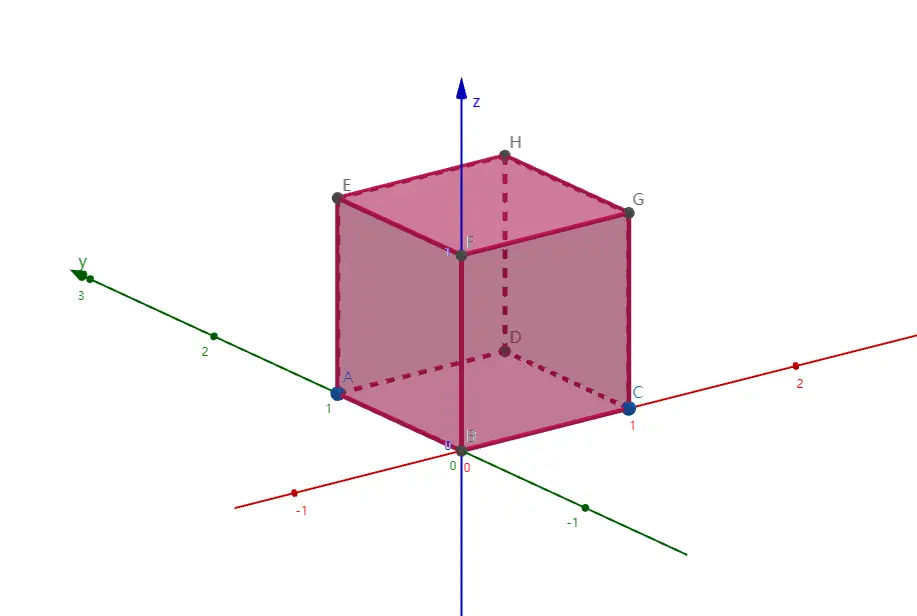
小 $\mathbf A$ 和小 $\mathbf B$ 各执一枚 $k$ 维空间中的点。

小 $\mathbf A$ 和小 $\mathbf B$ 轮流操作，小 $\mathbf A$ 先手。

定义一个维度为可操作的，当且仅当两个点中存在至少一个点在这个维度上的坐标不为 $0$。然后，操作方可以将两个点的某个可操作的维度的坐标置为 $0$。

如图，这是一个合法的操作：

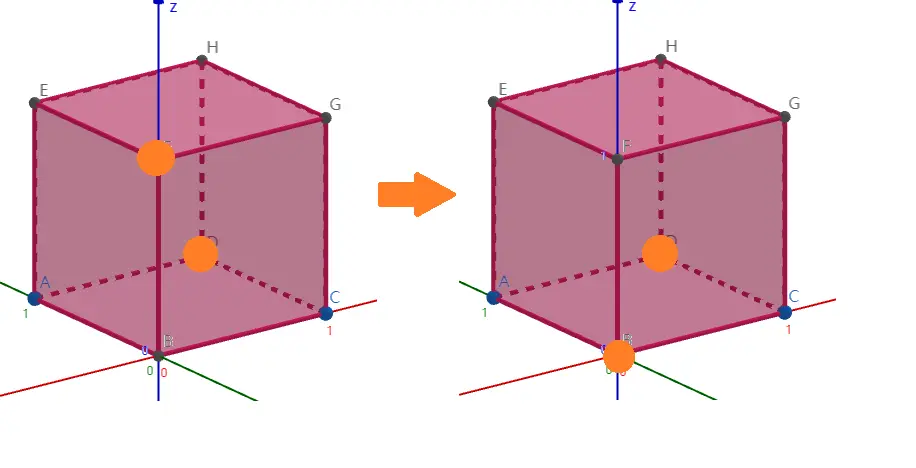
这也是一个合法的操作：

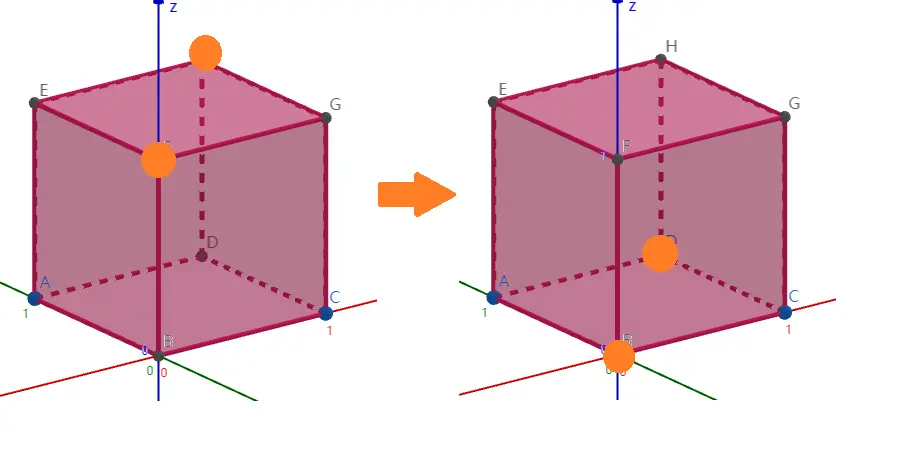
但是这不是一个合法的操作，因为两个点在这个维度上的坐标均为 $0$：

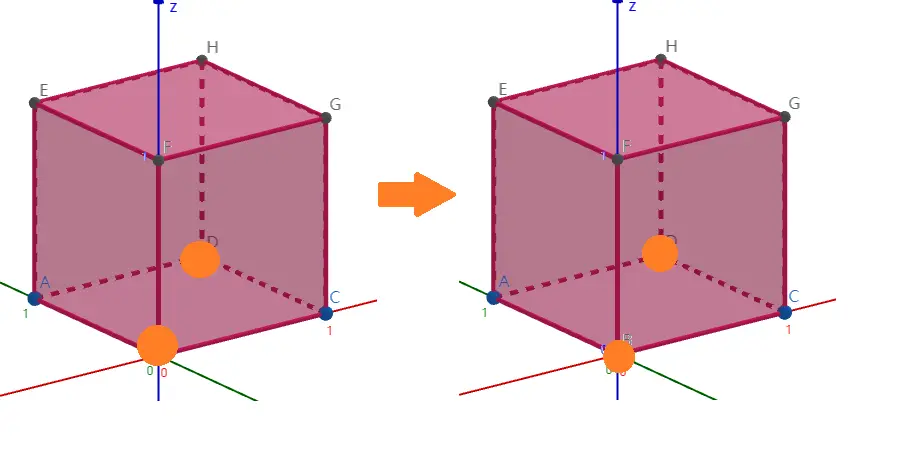
无法操作者输。

相信大家一定发现了，我们可以将任意一个坐标编码为一个二进制数。例如对于坐标 $(0,1,1,1,0,0,1,0)$，可以编码为 $\tt 01110010$，对应十进制数 $114$。

小 $\mathbf A$ 和 $\mathbf B$ 将进行 $q$ 轮游戏。两人绝顶聪明，都想要自己赢。每一轮双方点的位置将会随机生成，进一步地，生成到编码为 $x$ 的坐标的概率为 $p_x$。

由于小 $\mathbf A$ 先手，所以每轮她们将会划定一个可落子区域 $[l,r]$，其他区域则为不可落子区域。如果小 $\mathbf A$ 初始的点坐标编码后的值在区间 $[l,r]$ 外，则将会判为小 $\mathbf B$ 胜。（此规则对小 $\mathbf B$ 不生效，也就是即使小 $\mathbf B$ 初始的点坐标编码后的值在区间 $[l,r]$ 外，也不会直接判为小 $\mathbf A$ 胜）

现在对于第 $i$ 轮，可落子区域为 $[l_i,r_i]$，小 $\mathbf B$ 会有 $a_i$ 个询问，每个询问为当她的点被随机到编号为 $x$ 的坐标，且小 $\mathbf A$ 的点按照 $p$ 的概率随机生成时，她的胜率为多少。答案对 $998244353$ 取模。

输入格式

第一行一个正整数 $c$ 表示子任务编号，特殊地，样例的编号为 $0$。

接下来一行一个正整数 $t$ 表示数据读入输出方法。当 $t=1$ 时，你需要在下一行接着读入一个整数 $seed$ 表示随机种子。

接下来一行一个正整数 $k$ 表示维度数。

接下来一行 $2^k$ 个非负整数 $p_0,p_1,\cdots,p_{2^{k}-1}$ 表示生成到编码为 $x$ 的坐标的概率为 $p_x$。

接下来一行一个正整数 $q$ 表示游戏轮数。

接下来 $q$ 组询问，对于第 $i$ 组询问（下标从 $1$ 开始）：

每组询问第一行三个整数，表示 $a_i,l_i,r_i$。

当 $t=0$ 时，接下来一行 $a_i$ 个整数 $x_{i,1},x_{i,2},\cdots,x_{i,a_i}$，表示每次小 $\mathbf B$ 的询问。

当 $t=1$ 时，接下来小 $\mathbf B$ 的第 $j$ 个询问（下标从 $1$ 开始）$x_{i,j}$ 为 $seed\times i\times j\times 50007\bmod (2^k)$。

对于 C++ 选手，我们下发了一份数据读入模板 down.cpp，您只需要完善其中的代码部分即可。

输出格式

当 $t=0$ 时，对于第 $i$ 组询问输出一行 $a_i$ 个整数，表示这组询问所有答案模 $998244353$ 后的值。

当 $t=1$ 时，对于每组询问输出一行一个整数，表示这组询问所有答案模 $998244353$ 后的异或和。

0
0
2
0 1 998244351 2
2
1 2 3
2
2 0 1
2 3

3
1 1

0
1
50007
3
1 2 3 4 5 6 7 998244326
1
2 0 7

0

提示

样例 1 解释

对于第一组询问，当小 $\mathbf A$ 的点在编号为 $1$ 的坐标时，由于超出了可落子区域，小 $\mathbf B$ 胜；当小 $\mathbf A$ 的点在编号为 $2$ 的坐标时，小 $\mathbf A$ 胜；当小 $\mathbf A$ 的点在编号为 $3$ 的坐标时，小 $\mathbf B$ 胜。

故在模意义下，小 $\mathbf B$ 的胜率：$1+2=3$。

样例 2 解释

解码后，$x_{1,1}=1,x_{1,2}=2$，答案分别为 $18,18$，异或和为 $0$。

本题目采用捆绑测试。

子任务编号	$k\le$	$q\le$	$a_i\le$	时间限制	特殊性质	分值
$0$	$5$	$30$		1 秒	样例	$0$
$1$						$5$
$2$
$3$	$10$	$300$	$100$			$20$
$4$	$15$	$100$	$2^{15}$		$t=1$
$5$	$16$	$1000$	$100$			$10$
$6$		$2000$	$3000$		$t=1$
$7$		$3000$	$2^{15}$	2 秒		$30$

对于 $100\%$ 数据，满足 $1\le k\le 16,1\le q\le 3000,0\le p_i<998244353,1\le a_i\le 2^{15},0\le l_i\le r_i< 2^k,0\le x_{i,j}< 2^k,t\in\{0,1\},0\le seed\le 50007$。保证 $\sum_{i=0}^{2^k-1}p_i\equiv1\pmod{998244353}$。

本题输入输出量大，请使用较快的输入输出方式。