题目描述
房屋仲介小潮負責高談市的租房業務。小潮手上有編號為 1,2,⋯,n 的 n 間待租的房屋,房屋 i 的位置可以用二維座標 (ai,bi) 表示,並且此房屋的月租金為 ri 元。
高談市有 m 座捷運站,捷運站的編號為 1,2,⋯,m,捷運站 j 的位置在二維平面以座標 (cj,dj) 表示。定義房屋 i 與捷運站 j 的距離為 (ai−cj)2+(bi−dj)2 單位。
小潮發現租客的喜好如下:
- 房屋與最近的捷運站的距離越短越好。
- 如果兩間房屋和彼此最近的捷運站距離一樣近,月租金越小的房屋越好。
- 如果兩間房屋和彼此最近的捷運站距離一樣近,而且月租金相同,房屋編號越小的越好。
請幫忙小潮開發一個房屋推薦系統,對房屋們進行排序,使得越是得到租客喜愛的房屋排在越前面。
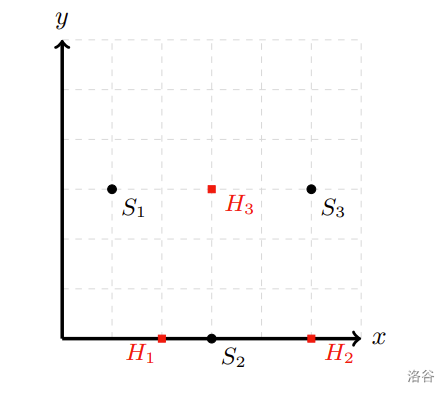
如下圖為一 n=3 且 m=3 的例子,其中正方形的點 H1,H2,H3 分別代表房屋 1,2,3,圓點 S1,S2,S3 則分別代表捷運站 1,2,3 的位置。並且:
- 第 1 間房屋位在 (2,0),月租金為 11000 元。
- 第 2 間房屋位在 (5,0),月租金為 12000 元。
- 第 3 間房屋位在 (3,3),月租金為 10000 元。
- 第 1 座捷運站位在 (1,3)。
- 第 2 座捷運站位在 (3,0)。
- 第 3 座捷運站位在 (5,3)。
可以算出:
- 和第 1 間房屋距離最短的捷運站為第 2 座捷運站,距離為 1 單位。
- 和第 2 間房屋距離最短的捷運站為第 2 座捷運站,距離為 2 單位。
- 和第 3 間房屋距離最短的捷運站為第 1 座捷運站與第 3 座捷運站,距離為 2 單位。
第 2 間房屋和第 3 間房屋和捷運站的距離都是 2 單位,但是因為第 3 間房屋的月租金較為便宜,所以排在第 2 間房屋前面。因此租客喜好的房屋順序為:1,3,2。
输入格式
n m
a1 b1 r1
a2 b2 r2
⋮
an bn rn
c1 d1
c2 d2
⋮
cm dm
- n, m 分別代表房屋與捷運站的數量。
- 房屋 i 的座標在 (ai,bi),且租金為 ri。
- 捷運站 j 的座標為 (cj,dj)。
输出格式
p1
p2
⋮
pn
- pi 為一整數,代表排名第 i 名的房屋編號。
3 3
2 0 11000
5 0 12000
3 3 10000
1 3
3 0
5 3
1
3
2
4 2
2 -2 10000
-2 1 12000
1 -3 12000
4 5 19000
1 5
4 1
4
1
2
3
提示
測資限制
- 1≤n≤105。
- 1≤m≤103。
- −109≤ai,bi,ci,di≤109。
- 0≤ri≤109
- 上述變數皆為整數。
- 任意一個座標最多只有一間房屋或一座捷運站,且不會有房屋和捷運站在同一座標。
評分說明
本題共有三組子任務,條件限制如下所示。
每一組可有一或多筆測試資料,該組所有測試資料皆需答對才會獲得該組分數。
| 子任務 |
分數 |
額外輸入限制 |
| 1 |
20 |
n≤2 |
| 2 |
30 |
n≤100 |
| 3 |
50 |
無額外限制 |

