- 题解
YIIC T3
- @ 2025-10-12 19:30:12
(标题还是忘了)
时间:1500ms
空间:512MB
文件:meet.in / .out
题面
有 座塔,塔之间一共有 条传送通道相连。这些传送通道可以双向通行,长度相同(可以认为是 个单位长度)。
有两个人分别在两座塔上,同时以最短路径以同样的速度向对方移动,问他们是在某座塔上相遇还是在某条传送通道上相遇?
现在共有 次询问,每次给定两个人初始所在的塔的编号 ,输出他们是在某座塔上相遇还是在某条传送通道上相遇。
输入
第一行,两个整数 。
接下来 行,每行两个整数 ,表示塔 和塔 之间有传送通道相连。
接下来 行,每行两个整数 ,代表一次询问。
输出
一共 行,对于第 行:
- 如果第 次询问中,两个人在塔上相遇,输出
Meet at the tower! - 否则,输出
Meeting at the passage!
nPr:这出题人英语不太行
数据范围
保证所有塔相互连通
nPr 赛时咋做的
每一个 都枚举一遍,用 BFS 预处理出最短路,放在神奇的双层 unordered_map 里(常数飞起来),取得 分高分
nPr 怎么AC的
首先,我们可以看到,塔之间一共有 条传送通道相连,并且保证所有塔相互连通。如果把塔看作结点,道路看作边,很明显这是一棵树。
如何判断两个人在路上还是在塔上相遇呢?只需判断奇偶性即可。
假设两人之间最短路的长度是 。
如果 是奇数,如下图:
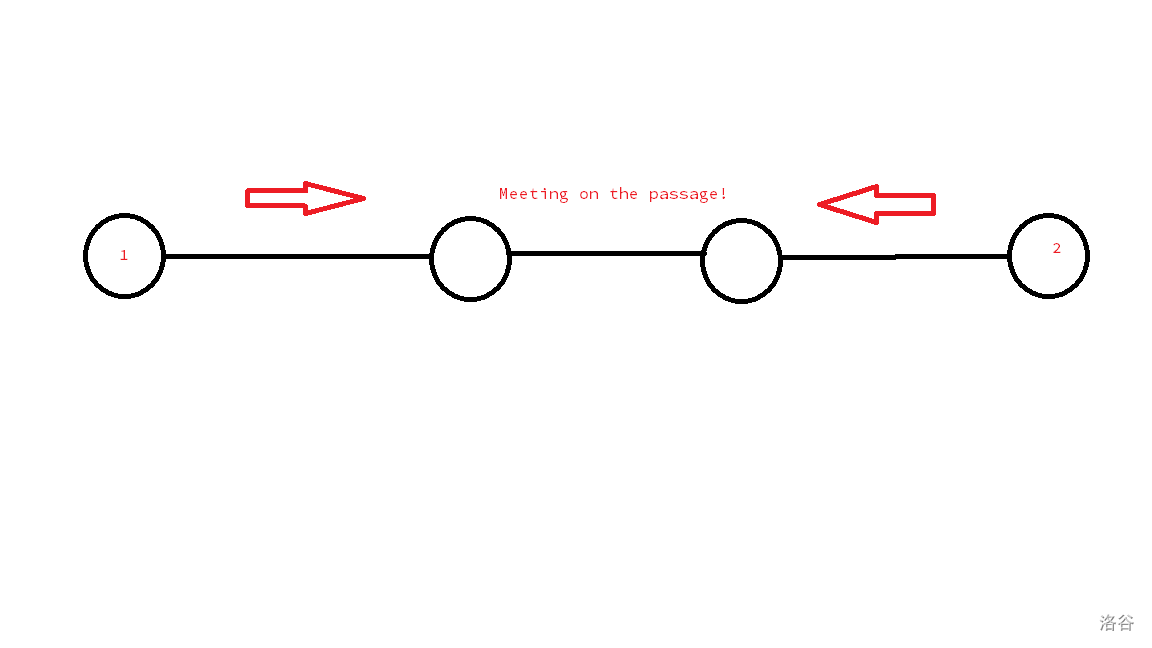
显然每个人都不可能走完整数条边,它们会在最中间那条边上相遇。
如果 是偶数,显然他们会在结点上相遇。
因此,问题便转化成:给定一棵树和 个二元组 ,计算 。
我们以下面这棵树为例:
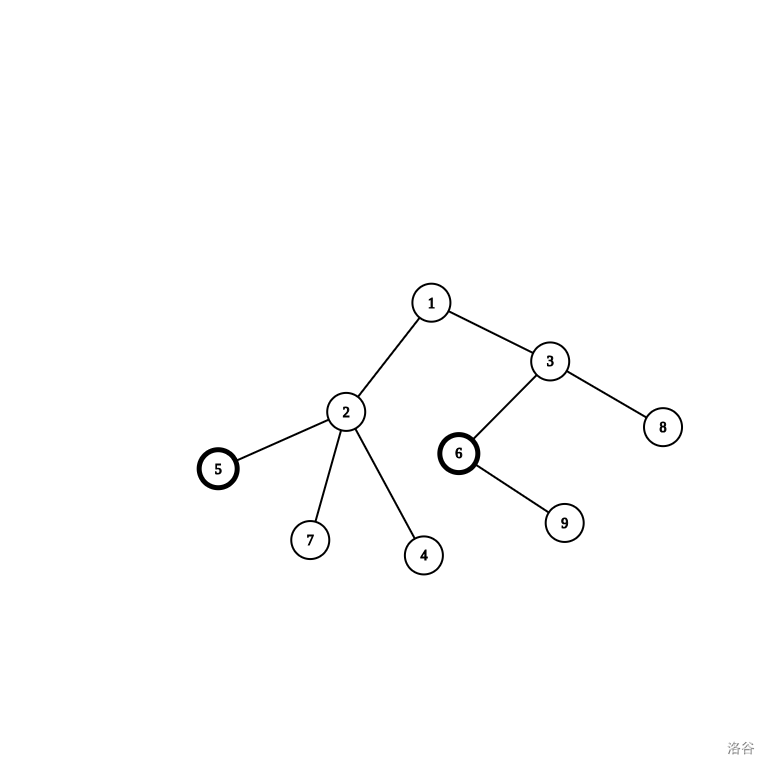
随便找几个点,算它们之间的最短路。
和 之间的最短路:。
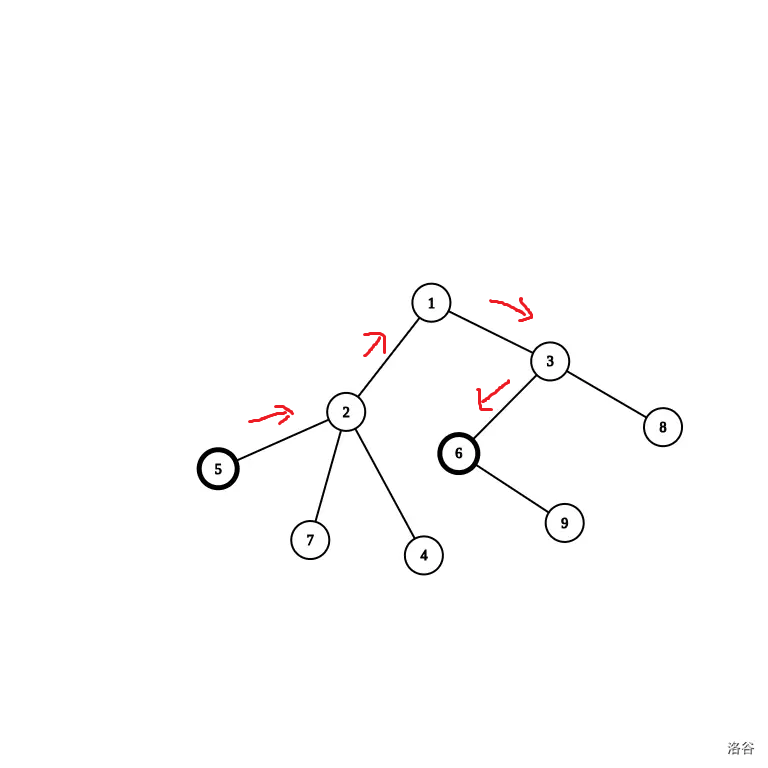
和 之间的最短路:。
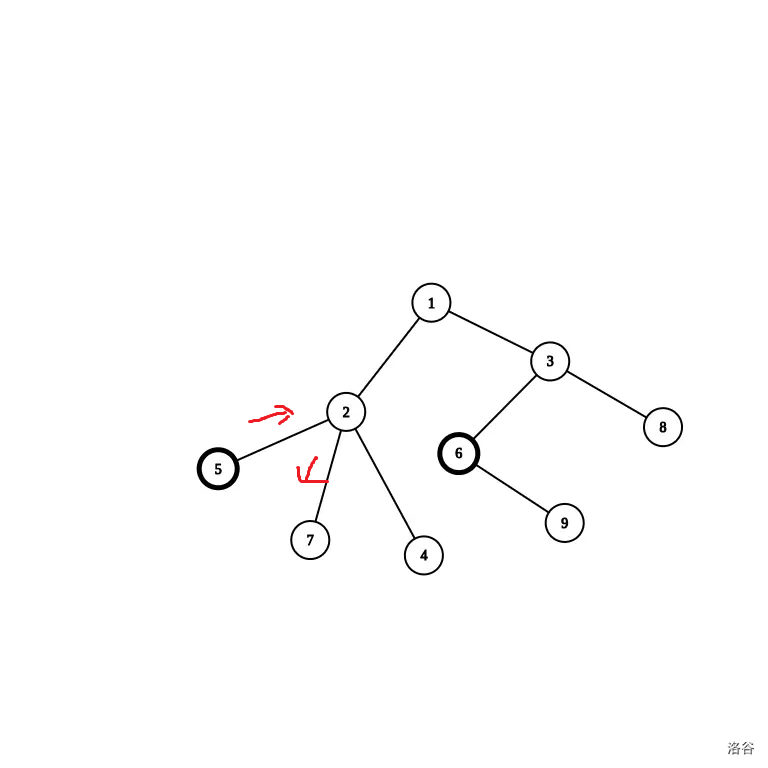
多找几个,我们可以发现,从任意一个起点 到任意一个终点 ,他们之间唯一的最短路径是先从 走到 和 的最近公共祖先 (两个节点的最近公共祖先,就是这两个点的公共祖先里面,离根最远的那个。如 和 的最近公共祖先是 )。再从 走到 。
如果我们单独考虑以 为根的子树,那么很显然, ( 表示以 为根的子树中结点 所在的深度),。
所以,问题又转化成了计算
但是, 一般用 Tarjan 之类的东西求,而 nPr123f 实在是太废物了,根本看不懂。
好像我是学过 Tarjan 的吧……
所以我们必须绕过 ,用另外的手段解决这个问题。
而问题的突破口就在前面公式最后的 上,只求奇偶性,这意味着我们并不需要求出完整最短路的长度。
我们怎么样才能用不多的学识解决这个问题呢?我们不妨考虑整棵树。
如果路径必须经过整棵树的根(这棵树的根为 ),那么 至 的最短路径将是 。
从 绕到根 ,又回到了 。
如果取消这个限制, 又有了另一种表达方式:
$$len(x, y) = deep(1, x) + deep(1, y) - 2 \times deep(1, LCA(x, y)) $$显然是偶数,不影响 的奇偶性。
因此。答案就是
而深度 (或者说 )很容易求,跑一遍 BFS,把所有的深度与处理出来就好了。
预处理时间复杂度 ,查询复杂度 ,非常优秀。
nPr Code
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
const int maxn = 1e5 + 10;
vector <int> g[maxn];
int dist[maxn];
bool vis[maxn];
struct Node {
int idx, dist;
};
int main() {
int n, q;
scanf("%d%d", &n, &q);
for (int i = 0; i < n - 1; i++) {
int m, n;
scanf("%d%d", &m, &n);
g[m].push_back(n);
g[n].push_back(m);
}
queue <Node> que;
que.push((Node){1, 0});
while (!que.empty()) {
Node f = que.front();
que.pop();
if (vis[f.idx]) continue;
vis[f.idx] = true;
dist[f.idx] = f.dist;
for (const auto& i : g[f.idx])
que.push((Node){i, f.dist + 1});
}
while (q--) {
int x, y;
scanf("%d%d", &x, &y);
puts((dist[x] + dist[y]) & 1 ? "Meeting on the passage!" : "Meet at the tower!");
}
return 0;
}
7 comments
-
C25lisihan LV 2 @ 2025-10-12 19:49:44
#include<bits/stdc++.h> using namespace std; int a[1000005]; int main() { int n, k; cin >> n >> k; for (int i=1;i<=n;i++) { cin >> a[i]; } sort(a+1, a+n+1); long long ans=0; for (int i=1;i<=n;i++) { int x=k^a[i]; int y=lower_bound(a+1, a+n+1, x)+a; int z=upper_bound(a+1, a+n+1, x)+a; if (y!=n&&z!=n) { ans+=y-z; } } cout << ans/2; return 0; } -
 @ 2025-10-12 19:44:17
@ 2025-10-12 19:44:17#include<bits/stdc++.h> using namespace std; long long a[100010]; int main(){ int n; long long k; cin>>n>>k; for(int i=1;i<=n;i++){ cin>>a[i]; } sort(a+1,a+1+n); int cnt=0; for(int i=1;i<=n;i++){ int id1=lower_bound(a+1,a+1+n,k^a[i])-a; int id2=upper_bound(a+1,a+1+n,k^a[i])-a; if(id1!=n&&id2!=n){ cnt+=id2-id1; } } cout<<cnt; return 0; } -
@ 2025-10-12 19:40:06
#include<iostream> #include<algorithm> using namespace std; long long n,k,a[1000010],b,s; int main(){ cin>>n>>k; for(int i=1;i<=n;i++){ cin>>a[i]; } sort(a+1,a+n+1); for(int i=1;i<=n;i++){ b=k^a[i]; long long p=lower_bound(a+1,a+n+1,b)-a; for(int j=p;j<=n&&a[j]==b;j++)s++; } cout<<s/2; return 0; } -
@ 2025-10-12 19:33:39
T2
#include<bits/stdc++.h> using namespace std; int a[1000005]; map<int, int> m; int main() { int n, k; cin >> n >> k; for (int i=1;i<=n;i++) { cin >> a[i]; m[a[i]]++; } long long ans=0; for (int i=1;i<=n;i++) { int x=k^a[i]; if (m[x]) { ans+=m[x]; } } cout << ans/2; return 0; }会炸
-
@ 2025-10-12 19:33:00
#include<bits/stdc++.h> using namespace std; int a[1000005]; map<int, int> m; int main() { int n, k; cin >> n >> k; for (int i=1;i<=n;i++) { cin >> a[i]; m[a[i]]++; } long long ans=0; for (int i=1;i<=n;i++) { int x=k^a[i]; if (m[x]) { ans+=m[x]; } } cout << ans/2; return 0; }
-
 @ 2025-10-12 19:31:39
@ 2025-10-12 19:31:39我是废物我先%%%
-
 @ 2025-10-12 19:31:07
@ 2025-10-12 19:31:07qp
- 1
