题目传送门

学习csp初赛精神，把简单的题做难

没绷住，考试时脑抽了写的o(nlogn)线段覆盖放这题会TLE20

首先我们可以拆分这个题目，先枚举区间再线段覆盖即可

那么如何枚举区间呢

可以用前缀和，循环枚举i和j去找区间[i+1,j]

因为对于任意的数$a,b,k$，若a ^ b == k，则a ^ k == b

所以我们可以先开一个unordered_map <ll,vector <ll> > mp，然后在循环输入时将i存进mp[a[i] ^ k]里，就可以用mp[a[j]]去找所有满足a[i] ^ a[j] == k的i

但是暴力还是太慢了，我考试时居然忽略了

所以我们想到对于所有的区间[i + 1,j]（其中j不变，$i < j$），显然只有最多一个区间被选上，此时i越大[i + 1,j]被选上的概率越高，这里可以直接unordered_map <ll,set <ll> > mp，然后用lower_bound或upper_bound去找即可，不过毕竟是要找最后一个小于j的数，所以要对以上两个函数变形

至于线段覆盖，如下图（）：

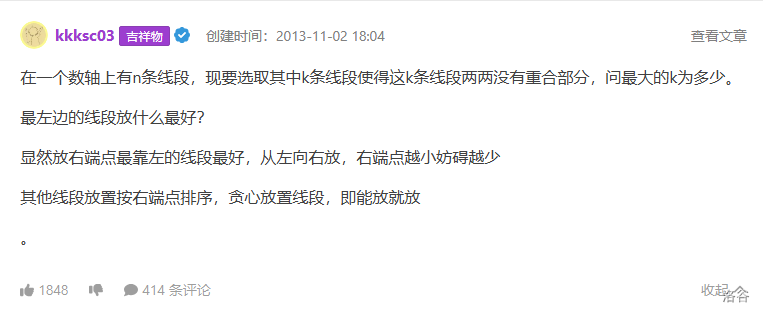
代码如下：

#include <iostream>
#include <unordered_map>
#include <vector>
#include <set>
#include <algorithm> 
using namespace std;
typedef long long ll;
const int N = 5e5 + 10;
struct pt{
    ll l,r;
};
ll n,k,dp_size;
bool chk;
ll a[N];//存前缀异或
unordered_map <ll,set <ll> > mp;//第一维存a[i] ^ k，第二维存符合第一维条件的i
vector <pt> cj;//存有用的区间
vector <ll> dp;//线段覆盖使用
bool cmp(pt a1,pt a2){
	return a1.r < a2.r;
}
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin >> n >> k;
    for (ll i = 1;i <= n;i++){
        cin >> a[i];
        a[i] ^= a[i - 1];
        if (a[i] == k && !chk){//检查有没有异或等于k的[1,i]区间，并把它们push进cj里
            cj.push_back(pt({1,i}));
            chk = 1;//假如已经存过了，那以后就不用存了，毕竟对于[1,i]和[1,j]（i<j）它们两个中只能有一个在线段覆盖中被选中，显然贪心存更小的区间合适，即存更小的i
        }
        mp[a[i] ^ k].insert(-i);
        //因为如果有a[i] ^ a[j] == k，那么a[i] ^ k == a[j]，不妨直接存a[i] ^ k，遍历a[j]去索引a[i] ^ k即可
        //存a[i] ^ k主要是方便直接用另一个a[j]去索引a[i]，使得a[i] ^ a[j] == k。换种方式：直接存a[i]，后面用a[j] ^ k索引亦可
        //插入i的相反数，用来找相反值最小的小于x的set里的数，用upper_bound即可
        //（删除线）不然还要手写平衡树，bro真的觉得我会
    }
    for (ll i = 1;i <= n;i++){
        auto j = mp[a[i]].upper_bound(-i);//找第一个小于i的下标j,同理，对于[x,i]和[y,i]（x<y）它们两个中只能有一个在线段覆盖中被选中，显然贪心存更小的区间合适，即存更大的y
        if (j != mp[a[i]].end() && -(*j) < i){
            cj.push_back(pt({-(*j) + 1,i}));
            //注意，a[i] ^ a[j] == (下标i + 1到j的所有数的异或值),所以要存j + 1
        }
    }
   // for (int i = 0;i < cj.size();i++){
   //     cout << cj[i].l << ' ' << cj[i].r << '\n';
   // }
   stable_sort(cj.begin(),cj.end(),cmp);
    dp.resize(cj.size() + 5);
    for (ll i = 0;i < cj.size();i++){//线段覆盖
    	if (dp[dp_size] < cj[i].l){
    		++dp_size;
    		dp[dp_size] = cj[i].r;
		}
    }
    cout << dp_size;
    return 0;
}

显然$O(nlogn)$的时间复杂度已经够ac了

但是看见题解区的dalao们竟然有时间复杂度为O(n)的解法，我感觉自己的代码还是太慢了

于是我想到我们可以在输入时就把枚举区间给搞定了

而且当我输入到i，通过mp索引到的异或a[i]等于k的a[j]时，我一定能保证j小于i（因为j是在之前的循环输入的），所以$j + 1 <= i$，即此时必定有区间[j + 1,i]的异或和等于k，这样就做到了$O(n)$的时间复杂度枚举。

假如有a[i] ^ k == a[i'] ^ k，（$i < i'$）那么直接用i'去覆盖掉i即可，甚至不用判断大小，因为是顺序输入

甚至因为是顺序输入，所以一定能保证枚举出的区间是有序的，你还可以直接在找到合适区间时就把线段覆盖做了

代码如下：

#include <iostream>
#include <unordered_map>
#include <vector>
#include <set>
#include <algorithm> 
using namespace std;
typedef long long ll;
const int N = 5e5 + 10;
struct pt{
    ll l,r;
};
ll n,k,dp_size;
bool chk;
ll a[N];
// unordered_map <ll,vector <ll> > mp;
unordered_map <ll,ll> mp;
vector <pt> cj;
vector <ll> dp;
bool cmp(pt a1,pt a2){
	return a1.r < a2.r;
}
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin >> n >> k;
    for (ll i = 1;i <= n;i++){
        cin >> a[i];
        a[i] ^= a[i - 1];
        if (a[i] == k && !chk){
            cj.push_back(pt({1,i}));
            chk = 1;
        }
        if (mp[a[i]])cj.push_back(pt({mp[a[i]] + 1,i}));
        mp[a[i] ^ k] = i;
        //毕竟一定是后来的，直接覆盖前面存的
//        cout << a[i] << ' ' << (a[i] ^ k) << ' ' << i << '\n';
    }
   // for (int i = 0;i < cj.size();i++){
   //     cout << cj[i].l << ' ' << cj[i].r << '\n';
   // }
   // stable_sort(cj.begin(),cj.end(),cmp);
  //既然都保证了区间有序，就不用排序了
    dp.resize(cj.size() + 5);
    for (ll i = 0;i < cj.size();i++){
    	if (dp[dp_size] < cj[i].l){
    		++dp_size;
    		dp[dp_size] = cj[i].r;
		}
    }
    cout << dp_size;
    return 0;
}